10. 一致性与共识
一句古老的格言告诫说:“千万不要带着两块计时器出海;要么带一块,要么带三块。”
弗雷德里克·P·布鲁克斯,《人月神话:软件工程随笔》(1995)
正如在 第九章 中讨论的,分布式系统中会出现许多问题。如果我们希望服务在出现这些问题时仍能正确工作,就需要找到容错的方法。
我们拥有的最佳容错工具之一是 复制。然而,正如我们在 第六章 中看到的,在多个副本上拥有多份数据副本会带来不一致的风险。读取可能由一个非最新的副本处理,从而产生过时的结果。如果多个副本可以接受写入,我们必须处理在不同副本上并发写入的值之间的冲突。从高层次来看,处理这些问题有两种相互竞争的理念:
- 最终一致性
- 在这种理念中,系统被复制这一事实对应用程序是可见的,作为应用程序开发者,你需要处理可能出现的不一致和冲突。这种方法通常用于多主复制(见 “多主复制”)和无主复制(见 “无主复制”)的系统中。
- 强一致性
- 这种理念认为应用程序不应该担心复制的内部细节,系统应该表现得就像单节点一样。这种方法的优点是对你(应用程序开发者)来说更简单。缺点是更强的一致性会带来性能成本,并且某些最终一致系统能够容忍的故障会导致强一致系统出现中断。
一如既往,哪种方法更好取决于你的应用程序。如果你有一个应用程序,用户可以在离线状态下对数据进行更改,那么最终一致性是不可避免的,如 “同步引擎与本地优先软件” 中所讨论的。然而,最终一致性对应用程序来说也可能很难处理。如果你的副本位于具有快速、可靠通信的数据中心,那么强一致性通常是合适的,因为其成本是可以接受的。
在本章中,我们将深入探讨强一致性方法,关注三个领域:
- 一个挑战是"强一致性"相当模糊,因此我们将制定一个更精确的定义,明确我们想要实现什么:线性一致性。
- 我们将研究生成 ID 和时间戳的问题。这可能听起来与一致性无关,但实际上密切相关。
- 我们将探讨分布式系统如何在保持容错的同时实现线性一致性;答案是 共识 算法。
在此过程中,我们将看到分布式系统中什么是可能的,什么是不可能的,存在一些基本限制。
本章的主题以难以正确实现而著称;构建在没有故障时表现良好,但在面对设计者没有考虑到的不幸故障组合时完全崩溃的系统非常容易。已经发展了大量理论来帮助我们思考这些边界情况,这使我们能够构建可以稳健地容忍故障的系统。
本章只会触及表面:我们将坚持非正式的直觉,避免算法细节、形式化模型和证明。如果你想在共识系统和类似基础设施上进行认真的工作,你需要更深入地研究理论,才有机会让你的系统稳健。与往常一样,本章中的文献参考提供了一些初步的指引。
线性一致性
如果你希望复制的数据库尽可能简单易用,你应该让它表现得就像根本没有复制一样。然后用户就不必担心复制延迟、冲突和其他不一致性。这将给我们带来容错的优势,但不会因为必须考虑多个副本而带来复杂性。
这就是 线性一致性 1 背后的想法(也称为 原子一致性 2、强一致性、即时一致性 或 外部一致性 3)。线性一致性的确切定义相当微妙,我们将在本节的其余部分探讨它。但基本思想是让系统看起来好像只有一份数据副本,并且对它的所有操作都是原子的。有了这个保证,即使实际上可能有多个副本,应用程序也不需要担心它们。
在线性一致系统中,一旦一个客户端成功完成写入,所有从数据库读取的客户端都必须能够看到刚刚写入的值。维护单一数据副本的假象意味着保证读取的值是最新的、最新的值,而不是来自过时的缓存或副本。换句话说,线性一致性是一个 新鲜度保证。为了阐明这个想法,让我们看一个非线性一致系统的例子。
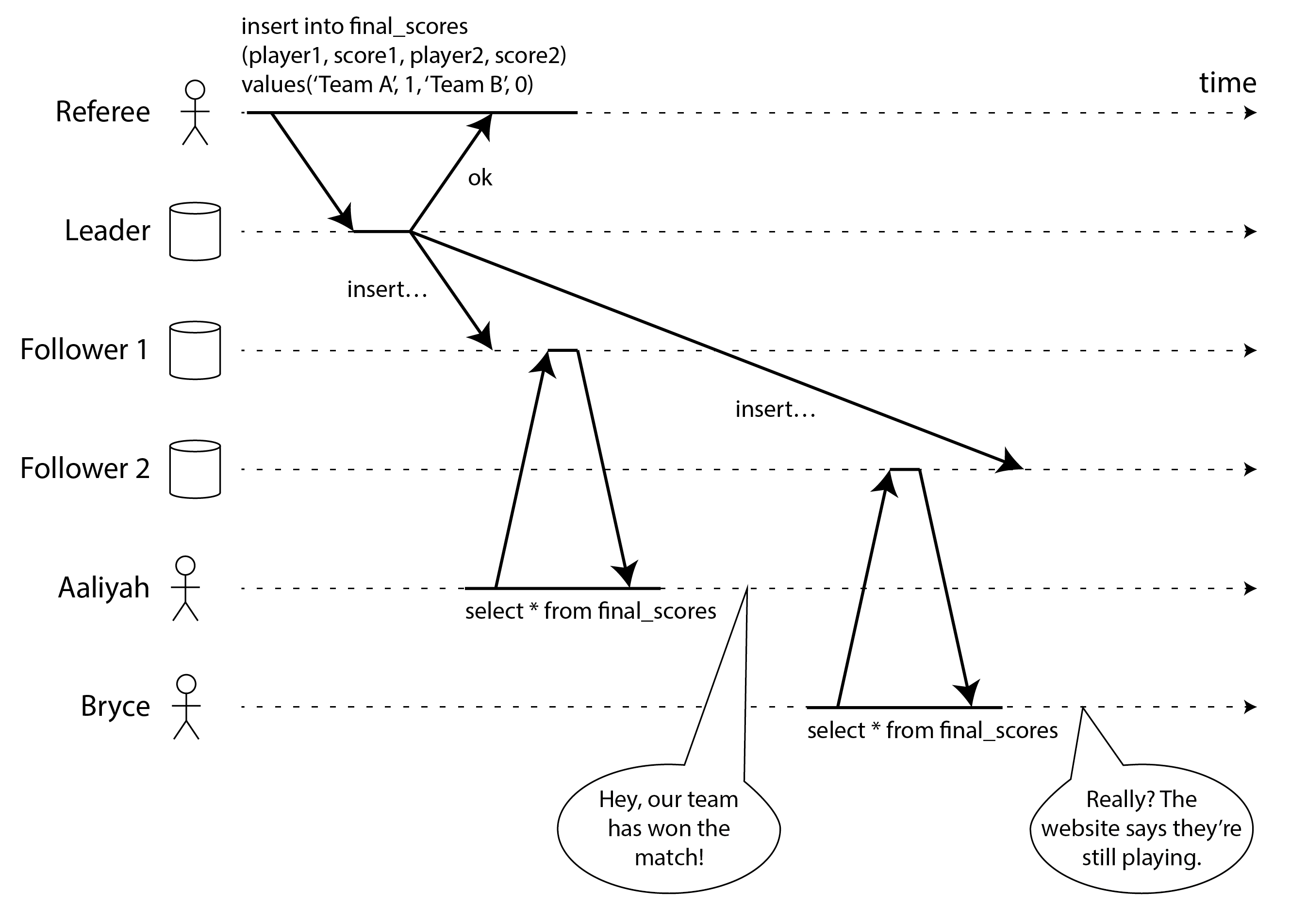
图 10-1 显示了一个非线性一致的体育网站示例 4。Aaliyah 和 Bryce 坐在同一个房间里,都在查看手机,想要了解他们最喜欢的球队比赛的结果。就在最终比分宣布后,Aaliyah 刷新了页面,看到了获胜者的公告,并兴奋地告诉了 Bryce。Bryce 怀疑地在自己的手机上点击了 刷新,但他的请求发送到了一个滞后的数据库副本,因此他的手机显示比赛仍在进行中。
如果 Aaliyah 和 Bryce 同时点击刷新,他们得到两个不同的查询结果就不会那么令人惊讶了,因为他们不知道他们各自的请求在服务器上被处理的确切时间。然而,Bryce 知道他是在听到 Aaliyah 宣布最终比分 之后 点击刷新按钮(发起查询)的,因此他期望他的查询结果至少与 Aaliyah 的一样新。他的查询返回过时结果这一事实违反了线性一致性。
什么使系统具有线性一致性?
为了更好地理解线性一致性,让我们看一些更多的例子。图 10-2 显示了三个客户端在线性一致数据库中并发读取和写入同一个对象 x。在分布式系统理论中,x 被称为 寄存器——在实践中,它可能是键值存储中的一个键,关系数据库中的一行,或者文档数据库中的一个文档,例如。
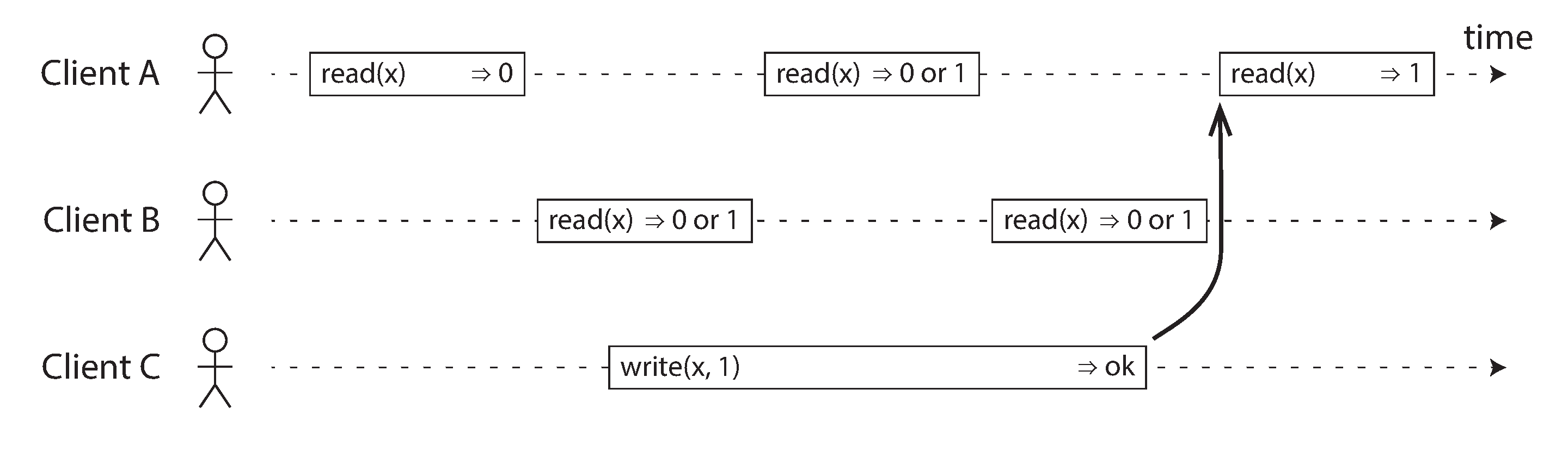
为简单起见,图 10-2 仅显示了从客户端角度看的请求,而不是数据库的内部。每个条形代表客户端发出的请求,条形的开始是发送请求的时间,条形的结束是客户端收到响应的时间。由于网络延迟可变,客户端不知道数据库确切何时处理了它的请求——它只知道必须在客户端发送请求和接收响应之间的某个时间发生。
在这个例子中,寄存器有两种类型的操作:
- read(x) ⇒ v 表示客户端请求读取寄存器 x 的值,数据库返回值 v。
- write(x, v) ⇒ r 表示客户端请求将寄存器 x 设置为值 v,数据库返回响应 r(可能是 ok 或 error)。
在 图 10-2 中,x 的值最初为 0,客户端 C 执行写入请求将其设置为 1。在此期间,客户端 A 和 B 反复轮询数据库以读取最新值。A 和 B 的读取请求可能得到什么响应?
- 客户端 A 的第一个读取操作在写入开始之前完成,因此它必须明确返回旧值 0。
- 客户端 A 的最后一次读取在写入完成后开始,因此如果数据库是线性一致的,它必须明确返回新值 1,因为读取必须在写入之后被处理。
- 与写入操作在时间上重叠的任何读取操作可能返回 0 或 1,因为我们不知道在读取操作被处理时写入是否已经生效。这些操作与写入是 并发 的。
然而,这还不足以完全描述线性一致性:如果与写入并发的读取可以返回旧值或新值,那么读者可能会在写入进行时多次看到值在旧值和新值之间来回翻转。这不是我们对模拟"单一数据副本"的系统所期望的。
为了使系统线性一致,我们需要添加另一个约束,如 图 10-3 所示。
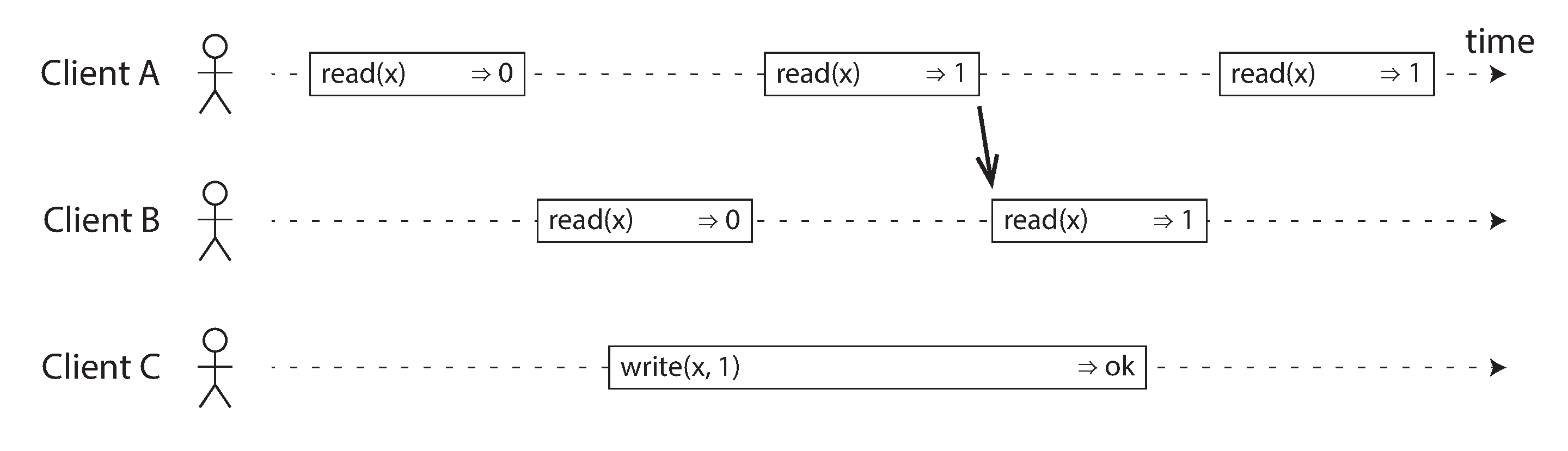
在线性一致系统中,我们想象必须有某个时间点(在写入操作的开始和结束之间),x 的值从 0 原子地翻转到 1。因此,如果一个客户端的读取返回新值 1,所有后续读取也必须返回新值,即使写入操作尚未完成。
这种时序依赖关系在 图 10-3 中用箭头表示。客户端 A 是第一个读取新值 1 的。就在 A 的读取返回后,B 开始新的读取。由于 B 的读取严格发生在 A 的读取之后,它也必须返回 1,即使 C 的写入仍在进行中。(这与 图 10-1 中 Aaliyah 和 Bryce 的情况相同:在 Aaliyah 读取新值后,Bryce 也期望读取新值。)
我们可以进一步细化这个时序图,以可视化每个操作在某个时间点原子地生效 5,就像 图 10-4 中显示的更复杂的例子。在这个例子中,除了 read 和 write 之外,我们添加了第三种操作类型:
- cas(x, vold, vnew) ⇒ r 表示客户端请求一个原子 比较并设置 操作(见 “条件写入(比较并设置)”)。如果寄存器 x 的当前值等于 vold,它应该原子地设置为 vnew。如果 x 的值与 vold 不同,则操作应该保持寄存器不变并返回错误。r 是数据库的响应(ok 或 error)。
图 10-4 中的每个操作都用一条垂直线(在每个操作的条形内)标记,表示我们认为操作执行的时间。这些标记按顺序连接起来,结果必须是寄存器的有效读写序列(每次读取必须返回最近写入设置的值)。
线性一致性的要求是连接操作标记的线始终向前移动(从左到右),永不后退。这个要求确保了我们之前讨论的新鲜度保证:一旦写入或读取了新值,所有后续读取都会看到写入的值,直到它再次被覆盖。
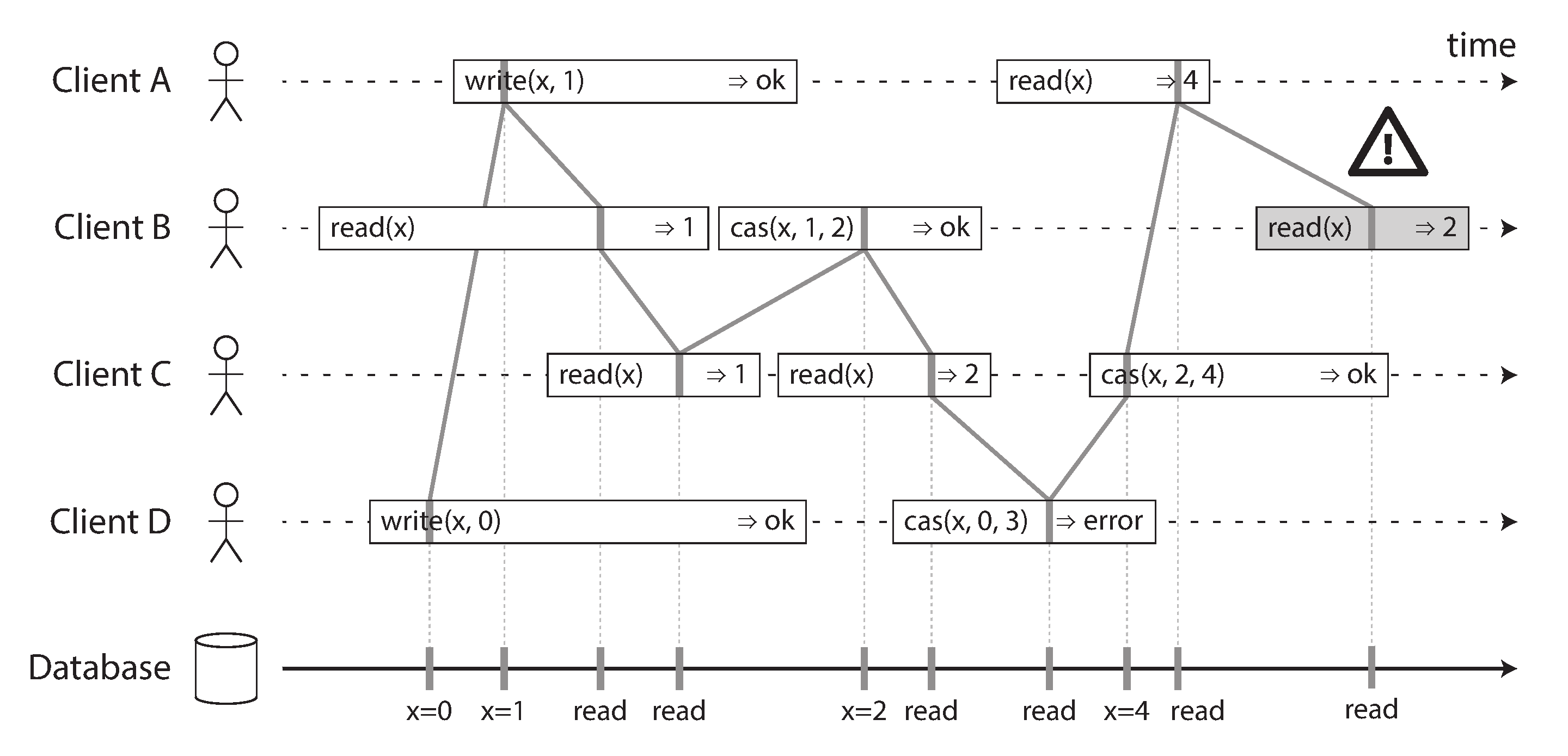
图 10-4 中有一些有趣的细节需要指出:
- 首先客户端 B 发送了读取 x 的请求,然后客户端 D 发送了将 x 设置为 0 的请求,然后客户端 A 发送了将 x 设置为 1 的请求。然而,返回给 B 的读取值是 1(A 写入的值)。这是可以的:这意味着数据库首先处理了 D 的写入,然后是 A 的写入,最后是 B 的读取。虽然这不是发送请求的顺序,但这是一个可接受的顺序,因为这三个请求是并发的。也许 B 的读取请求在网络中稍有延迟,因此它在两次写入之后才到达数据库。
- 客户端 B 的读取在客户端 A 收到数据库的响应之前返回了 1,表示值 1 的写入成功。这也是可以的:这只是意味着从数据库到客户端 A 的 ok 响应在网络中稍有延迟。
- 这个模型不假设任何事务隔离:另一个客户端可以随时更改值。例如,C 首先读取 1,然后读取 2,因为该值在两次读取之间被 B 更改了。原子比较并设置(cas)操作可用于检查值是否未被另一个客户端并发更改:B 和 C 的 cas 请求成功,但 D 的 cas 请求失败(到数据库处理它时,x 的值不再是 0)。
- 客户端 B 的最后一次读取(在阴影条中)不是线性一致的。该操作与 C 的 cas 写入并发,后者将 x 从 2 更新到 4。在没有其他请求的情况下,B 的读取返回 2 是可以的。然而,客户端 A 在 B 的读取开始之前已经读取了新值 4,因此 B 不允许读取比 A 更旧的值。同样,这与 图 10-1 中 Aaliyah 和 Bryce 的情况相同。
这就是线性一致性背后的直觉;形式化定义 1 更精确地描述了它。可以(尽管计算成本高昂)通过记录所有请求和响应的时序,并检查它们是否可以排列成有效的顺序序列来测试系统的行为是否线性一致 6 7。
就像除了可串行化之外还有各种弱隔离级别用于事务(见 “弱隔离级别”),除了线性一致性之外,复制系统也有各种较弱的一致性模型 8。实际上,我们在 “复制延迟问题” 中看到的 写后读、单调读 和 一致性前缀读 属性就是这种较弱一致性模型的例子。线性一致性保证所有这些较弱的属性,以及更多。在本章中,我们将重点关注线性一致性,它是最常用的最强一致性模型。
线性一致性与可串行化
线性一致性很容易与可串行化混淆(见 “可串行化”),因为这两个词似乎都意味着类似"可以按顺序排列"的东西。然而,它们是完全不同的保证,区分它们很重要:
- 可串行化
- 可串行化是事务的隔离属性,其中每个事务可能读取和写入 多个对象(行、文档、记录)。它保证事务的行为与它们按 某种 串行顺序执行时相同:也就是说,就好像你首先执行一个事务的所有操作,然后执行另一个事务的所有操作,依此类推,而不交错它们。该串行顺序可以与事务实际运行的顺序不同 9。
- 线性一致性
- 线性一致性是对寄存器(单个对象)的读写保证。它不将操作分组到事务中,因此它不能防止涉及多个对象的问题,如写偏差(见 “写偏差和幻读”)。然而,线性一致性是一个 新鲜度 保证:它要求如果一个操作在另一个操作开始之前完成,那么后一个操作必须观察到至少与前一个操作一样新的状态。可串行化没有这个要求:例如,可串行化允许过时读取 10。
(顺序一致性 又是另外一回事 8,但我们不会在这里讨论它。)
数据库可能同时提供可串行化和线性一致性,这种组合称为 严格可串行化 或 强单副本可串行化(strong-1SR)11 12。单节点数据库通常是线性一致的。对于使用乐观方法(如可串行化快照隔离)的分布式数据库(见 “可串行化快照隔离(SSI)”),情况更加复杂:例如,CockroachDB 提供可串行化和对读取的一些新鲜度保证,但不是严格可串行化 13,因为这需要事务之间进行昂贵的协调 14。
也可以将较弱的隔离级别与线性一致性结合,或将较弱的一致性模型与可串行化结合;实际上,一致性模型和隔离级别可以在很大程度上相互独立地选择 15 16。
依赖线性一致性
在什么情况下线性一致性有用?查看体育比赛的最终比分也许是一个无关紧要的例子:过时几秒钟的结果在这种情况下不太可能造成任何实际伤害。然而,有几个领域中线性一致性是使系统正确工作的重要要求。
锁定与领导者选举
使用单主复制的系统需要确保确实只有一个主节点,而不是多个(脑裂)。选举领导者的一种方法是使用租约:每个启动的节点都尝试获取租约,成功的节点成为领导者 17。无论这种机制如何实现,它都必须是线性一致的:两个不同的节点不应该能够同时获取租约。
像 Apache ZooKeeper 18 和 etcd 这样的协调服务通常用于实现分布式租约和领导者选举。它们使用共识算法以容错的方式实现线性一致的操作(我们将在本章后面讨论这些算法)。实现租约和领导者选举正确仍然有许多微妙的细节(例如,参见 “分布式锁和租约” 中的栅栏问题),像 Apache Curator 这样的库通过在 ZooKeeper 之上提供更高级别的配方来提供帮助。然而,线性一致的存储服务是这些协调任务的基本基础。
Note
严格来说,ZooKeeper 提供线性一致的写入,但读取可能是过时的,因为不能保证它们由当前领导者提供 18。etcd 从版本 3 开始默认提供线性一致的读取。
分布式锁也在一些分布式数据库中以更细粒度的级别使用,例如 Oracle Real Application Clusters (RAC) 19。RAC 对每个磁盘页使用一个锁,多个节点共享对同一磁盘存储系统的访问。由于这些线性一致的锁位于事务执行的关键路径上,RAC 部署通常具有专用的集群互连网络用于数据库节点之间的通信。
约束与唯一性保证
唯一性约束在数据库中很常见:例如,用户名或电子邮件地址必须唯一标识一个用户,在文件存储服务中不能有两个具有相同路径和文件名的文件。如果你想在数据写入时强制执行此约束(这样如果两个人同时尝试创建具有相同名称的用户或文件,其中一个将返回错误),你需要线性一致性。
这种情况实际上类似于锁:当用户注册你的服务时,你可以认为他们获取了所选用户名的"锁"。该操作也非常类似于原子比较并设置,将用户名设置为声明它的用户的 ID,前提是用户名尚未被占用。
如果你想确保银行账户余额永远不会变为负数,或者你不会销售超过仓库库存的物品,或者两个人不会同时预订同一航班或剧院的同一座位,也会出现类似的问题。这些约束都要求有一个所有节点都同意的单一最新值(账户余额、库存水平、座位占用情况)。
在实际应用中,有时可以接受宽松地对待这些约束(例如,如果航班超售,你可以将客户转移到其他航班,并为不便提供补偿)。在这种情况下,可能不需要线性一致性,我们将在 [Link to Come] 中讨论这种宽松解释的约束。
然而,硬唯一性约束,例如你通常在关系数据库中找到的约束,需要线性一致性。其他类型的约束,例如外键或属性约束,可以在没有线性一致性的情况下实现 20。
跨通道时序依赖
注意 图 10-1 中的一个细节:如果 Aaliyah 没有大声说出比分,Bryce 就不会知道他的查询结果是过时的。他只会在几秒钟后再次刷新页面,最终看到最终比分。线性一致性违规之所以被注意到,只是因为系统中有一个额外的通信通道(Aaliyah 的声音到 Bryce 的耳朵)。
类似的情况可能出现在计算机系统中。例如,假设你有一个网站,用户可以上传视频,后台进程将视频转码为较低质量,以便在慢速互联网连接上流式传输。该系统的架构和数据流如 图 10-5 所示。
视频转码器需要明确指示执行转码作业,此指令通过消息队列从 Web 服务器发送到转码器(见 [Link to Come])。Web 服务器不会将整个视频放在队列中,因为大多数消息代理都是为小消息设计的,而视频可能有许多兆字节大小。相反,视频首先写入文件存储服务,写入完成后,转码指令被放入队列。
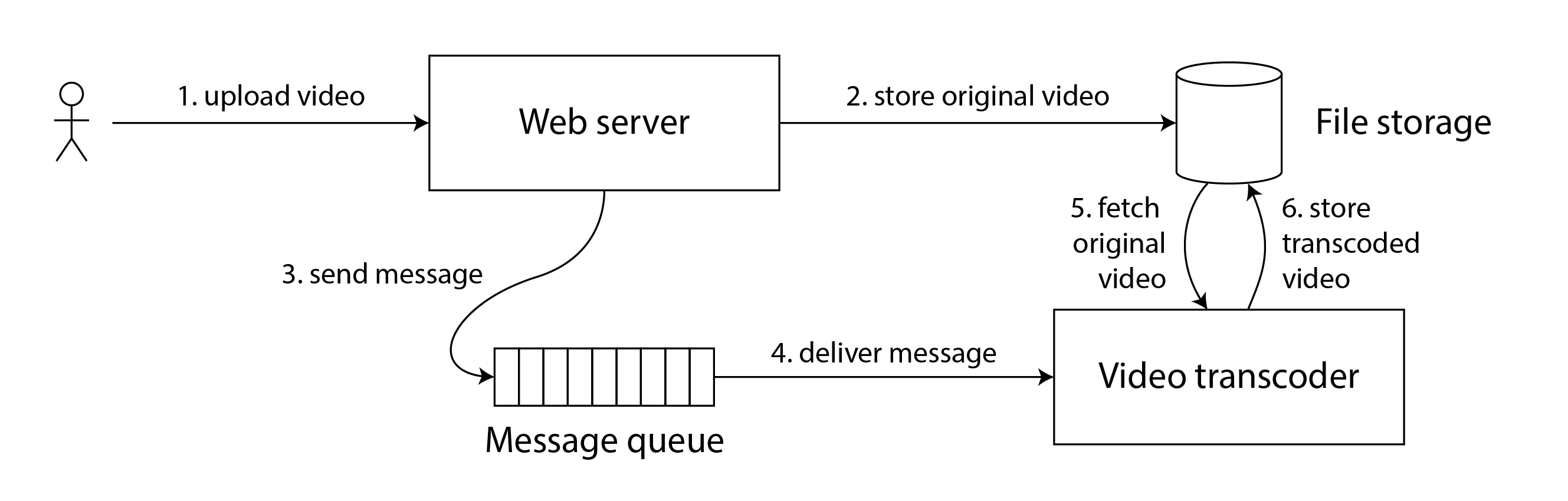
如果文件存储服务是线性一致的,那么这个系统应该工作正常。如果它不是线性一致的,就存在竞态条件的风险:消息队列(图 10-5 中的步骤 3 和 4)可能比存储服务内部的复制更快。在这种情况下,当转码器获取原始视频(步骤 5)时,它可能会看到文件的旧版本,或者根本看不到任何内容。如果它处理视频的旧版本,文件存储中的原始视频和转码视频将永久不一致。
这个问题的出现是因为 Web 服务器和转码器之间有两个不同的通信通道:文件存储和消息队列。如果没有线性一致性的新鲜度保证,这两个通道之间可能存在竞态条件。这种情况类似于 图 10-1,其中也存在两个通信通道之间的竞态条件:数据库复制和 Aaliyah 嘴巴到 Bryce 耳朵之间的现实音频通道。
如果你有一个可以接收推送通知的移动应用程序,并且应用程序在收到推送通知时从服务器获取一些数据,就会发生类似的竞态条件。如果数据获取可能发送到滞后的副本,可能会发生推送通知快速通过,但后续获取没有看到推送通知所涉及的数据。
线性一致性不是避免这种竞态条件的唯一方法,但它是最容易理解的。如果你控制额外的通信通道(如消息队列的情况,但不是 Aaliyah 和 Bryce 的情况),你可以使用类似于我们在 “读己之写” 中讨论的替代方法,但代价是额外的复杂性。
实现线性一致性系统
现在我们已经看了线性一致性有用的几个例子,让我们思考如何实现一个提供线性一致语义的系统。
由于线性一致性本质上意味着"表现得好像只有一份数据副本,并且对它的所有操作都是原子的",最简单的答案是真的只使用一份数据副本。然而,这种方法将无法容忍故障:如果持有该副本的节点失败,数据将丢失,或者至少在节点重新启动之前无法访问。
让我们重新审视 第六章 中的复制方法,并比较它们是否可以实现线性一致:
- 单主复制(可能线性一致)
- 在单主复制系统中,主节点拥有用于写入的数据主副本,从节点在其他节点上维护数据的备份副本。只要你在主节点上执行所有读写操作,它们很可能是线性一致的。然而,这假设你确定知道谁是主节点。如 “分布式锁和租约” 中所讨论的,一个节点很可能认为自己是主节点,而实际上并不是——如果这个妄想的主节点继续服务请求,很可能会违反线性一致性 21。使用异步复制,故障切换甚至可能丢失已提交的写入,这违反了持久性和线性一致性。
对单主数据库进行分片,每个分片有一个单独的主节点,不会影响线性一致性,因为它只是单对象保证。跨分片事务是另一回事(见 “分布式事务”)。
- 共识算法(可能线性一致)
- 一些共识算法本质上是带有自动领导者选举和故障切换的单主复制。它们经过精心设计以防止脑裂,使它们能够安全地实现线性一致的存储。ZooKeeper 使用 Zab 共识算法 22,etcd 使用 Raft 23,例如。然而,仅仅因为系统使用共识并不能保证其上的所有操作都是线性一致的:如果它允许在不检查节点是否仍然是领导者的情况下在节点上读取,读取的结果可能是过时的,如果刚刚选出了新的领导者。
- 多主复制(非线性一致)
- 具有多主复制的系统通常不是线性一致的,因为它们在多个节点上并发处理写入,并将它们异步复制到其他节点。因此,它们可能产生需要解决的冲突写入(见 “处理冲突写入”)。
- 无主复制(可能非线性一致)
- 对于具有无主复制的系统(Dynamo 风格;见 “无主复制”),人们有时声称可以通过要求仲裁读写(w + r > n)来获得"强一致性"。根据确切的算法,以及你如何定义强一致性,这并不完全正确。
基于日历时钟的"最后写入获胜"冲突解决方法(例如,在 Cassandra 和 ScyllaDB 中)几乎肯定是非线性一致的,因为时钟时间戳由于时钟偏差而无法保证与实际事件顺序一致(见 “依赖同步时钟”)。即使使用仲裁,也可能出现非线性一致的行为,如下一节所示。
线性一致性与仲裁
直观地说,在 Dynamo 风格的模型中,仲裁读写似乎应该是线性一致的。然而,当我们有可变的网络延迟时,可能会出现竞态条件,如 图 10-6 所示。
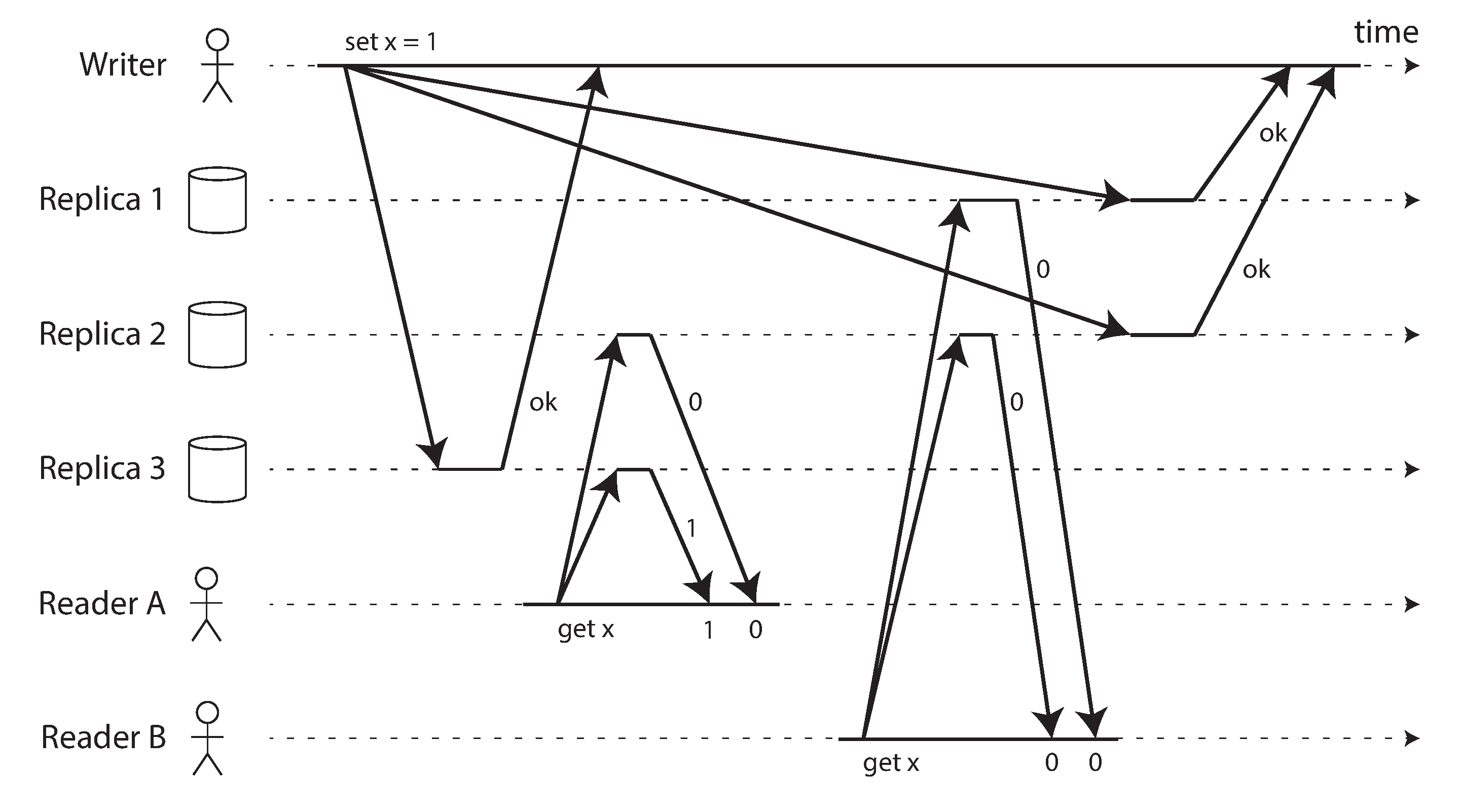
在 图 10-6 中,x 的初始值为 0,写入客户端通过向所有三个副本发送写入(n = 3,w = 3)将 x 更新为 1。同时,客户端 A 从两个节点的仲裁(r = 2)读取,并在其中一个节点上看到新值 1。同时与写入并发,客户端 B 从不同的两个节点仲裁读取,并从两者获得旧值 0。
仲裁条件得到满足(w + r > n),但这种执行仍然不是线性一致的:B 的请求在 A 的请求完成后开始,但 B 返回旧值而 A 返回新值。(这又是 图 10-1 中 Aaliyah 和 Bryce 的情况。)
可以使 Dynamo 风格的仲裁线性一致,但代价是降低性能:读者必须同步执行读修复(见 “追赶错过的写入”),然后才能将结果返回给应用程序 24。此外,在写入之前,写入者必须读取节点仲裁的最新状态以获取任何先前写入的最新时间戳,并确保新写入具有更大的时间戳 25 26。然而,Riak 由于性能损失而不执行同步读修复。Cassandra 确实等待仲裁读取时的读修复完成 27,但由于它使用日历时钟作为时间戳而失去了线性一致性。
此外,只有线性一致的读写操作可以以这种方式实现;线性一致的比较并设置操作不能,因为它需要共识算法 28。
总之,最安全的假设是,具有 Dynamo 风格复制的无主系统不提供线性一致性,即使使用仲裁读写。
线性一致性的代价
由于某些复制方法可以提供线性一致性而其他方法不能,因此更深入地探讨线性一致性的利弊是很有趣的。
我们已经在 第六章 中讨论了不同复制方法的一些用例;例如,我们看到多主复制通常是多区域复制的良好选择(见 “地理分布式操作”)。图 10-7 展示了这种部署的示例。
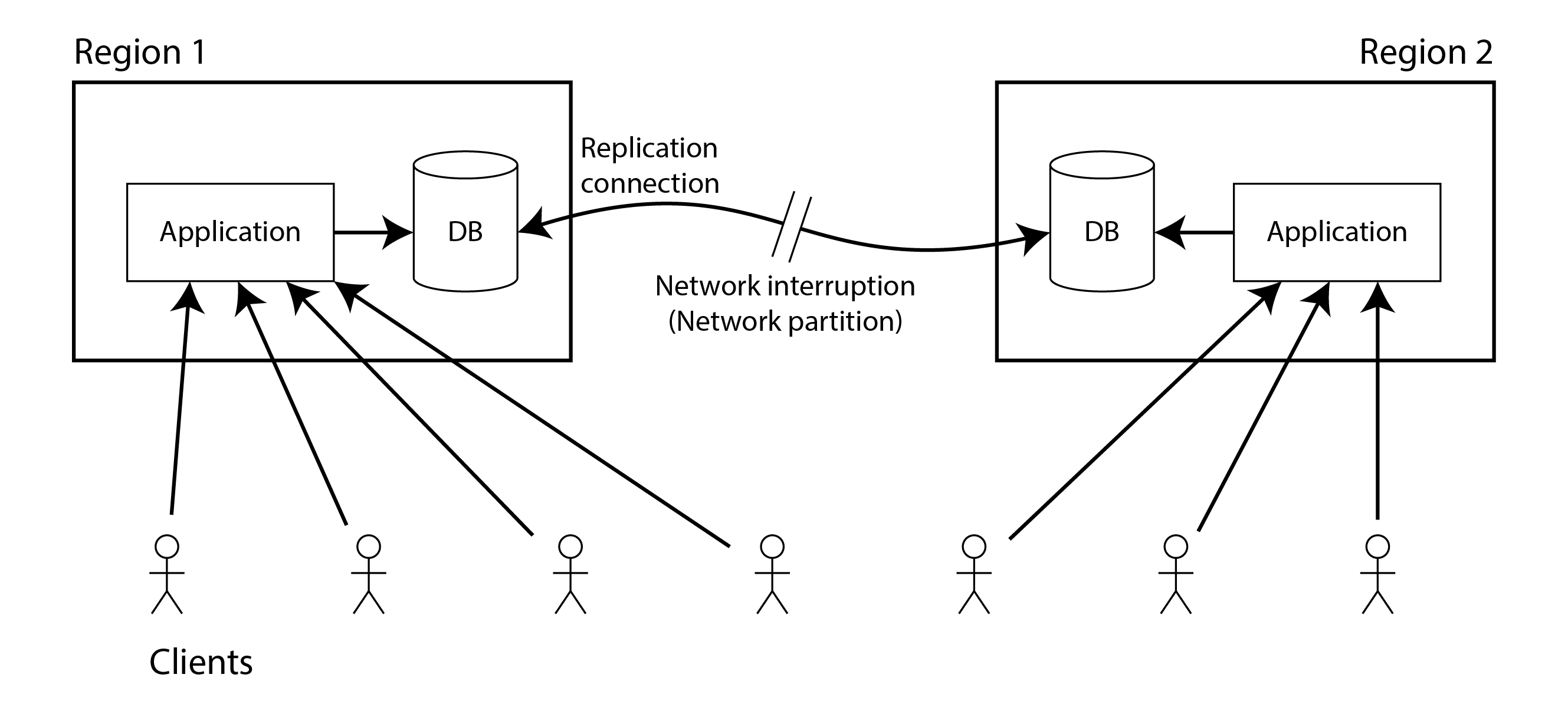
考虑如果两个区域之间出现网络中断会发生什么。让我们假设每个区域内的网络正常工作,客户端可以到达其本地区域,但这些区域之间无法相互连接。这被称为 网络分区。
使用多主数据库,每个区域可以继续正常运行:由于来自一个区域的写入被异步复制到另一个区域,写入只是排队并在网络连接恢复时交换。
另一方面,如果使用单主复制,那么主节点必须在其中一个区域。任何写入和任何线性一致的读取都必须发送到主节点——因此,对于连接到从节点区域的任何客户端,这些读写请求必须通过网络同步发送到主节点区域。
如果在单主设置中区域之间的网络中断,连接到从节点区域的客户端无法联系主节点,因此它们既不能对数据库进行任何写入,也不能进行任何线性一致的读取。它们仍然可以从从节点读取,但它们可能是过时的(非线性一致)。如果应用程序需要线性一致的读写,网络中断会导致应用程序在无法联系主节点的区域中变得不可用。
如果客户端可以直接连接到主节点区域,这不是问题,因为应用程序在那里继续正常工作。但只能访问从节点区域的客户端将在网络链接修复之前遇到中断。
CAP 定理
这个问题不仅仅是单主和多主复制的结果:任何线性一致的数据库都有这个问题,无论它如何实现。这个问题也不特定于多区域部署,而是可以发生在任何不可靠的网络上,即使在一个区域内。权衡如下:
- 如果你的应用程序 需要 线性一致性,并且某些副本由于网络问题与其他副本断开连接,那么某些副本在断开连接时无法处理请求:它们必须等待网络问题修复,或者返回错误(无论哪种方式,它们都变得 不可用)。这种选择有时被称为 CP(在网络分区下一致)。
- 如果你的应用程序 不需要 线性一致性,那么它可以以一种方式编写,使每个副本可以独立处理请求,即使它与其他副本断开连接(例如,多主)。在这种情况下,应用程序可以在面对网络问题时保持 可用,但其行为不是线性一致的。这种选择被称为 AP(在网络分区下可用)。
因此,不需要线性一致性的应用程序可以更好地容忍网络问题。这种见解通常被称为 CAP 定理 29 30 31 32,由 Eric Brewer 在 2000 年命名,尽管这种权衡自 1970 年代以来就为分布式数据库设计者所知 33 34 35。
CAP 最初是作为经验法则提出的,没有精确的定义,目的是开始关于数据库中权衡的讨论。当时,许多分布式数据库专注于在具有共享存储的机器集群上提供线性一致语义 19,CAP 鼓励数据库工程师探索更广泛的分布式无共享系统设计空间,这些系统更适合实现大规模 Web 服务 36。CAP 在这种文化转变方面值得称赞——它帮助触发了 NoSQL 运动,这是 2000 年代中期左右的一系列新数据库技术。
无用的 CAP 定理
CAP 有时被表述为 一致性、可用性、分区容错性:从 3 个中选择 2 个。不幸的是,这样表述是误导性的 32,因为网络分区是一种故障,所以它们不是你可以选择的:无论你喜欢与否,它们都会发生。
当网络正常工作时,系统可以同时提供一致性(线性一致性)和完全可用性。当发生网络故障时,你必须在线性一致性或完全可用性之间进行选择。因此,CAP 的更好表述方式是 分区时要么一致要么可用 37。更可靠的网络需要更少地做出这种选择,但在某个时候这种选择是不可避免的。
CP/AP 分类方案还有几个进一步的缺陷 4。一致性 被形式化为线性一致性(定理没有说任何关于较弱一致性模型的内容),可用性 的形式化 30 与该术语的通常含义不匹配 38。许多高可用(容错)系统实际上不符合 CAP 对可用性的特殊定义。此外,一些系统设计者选择(有充分理由)既不提供线性一致性也不提供 CAP 定理假设的可用性形式,因此这些系统既不是 CP 也不是 AP 39 40。
总的来说,关于 CAP 有很多误解和混淆,它并不能帮助我们更好地理解系统,因此最好避免使用 CAP。
正式定义的 CAP 定理 30 范围非常狭窄:它只考虑一种一致性模型(即线性一致性)和一种故障(网络分区,根据 Google 的数据,这是不到 8% 事件的原因 41)。它没有说任何关于网络延迟、死节点或其他权衡的内容。因此,尽管 CAP 在历史上具有影响力,但对于设计系统几乎没有实际价值 4 38。
已经有努力推广 CAP。例如,PACELC 原则 观察到系统设计者也可能选择在网络正常工作时削弱一致性以减少延迟 39 40 42。因此,在网络分区(P)期间,我们需要在可用性(A)和一致性(C)之间进行选择;否则(E),当没有分区时,我们可能在低延迟(L)和一致性(C)之间进行选择。然而,这个定义继承了 CAP 的几个问题,例如一致性和可用性的反直觉定义。
分布式系统中有许多更有趣的不可能性结果 43,CAP 现在已被更精确的结果所取代 44 45,因此它今天主要具有历史意义。
线性一致性与网络延迟
尽管线性一致性是一个有用的保证,但令人惊讶的是,实际上很少有系统是线性一致的。例如,即使现代多核 CPU 上的 RAM 也不是线性一致的 46:如果在一个 CPU 核心上运行的线程写入内存地址,而另一个 CPU 核心上的线程随后读取相同的地址,不能保证读取第一个线程写入的值(除非使用 内存屏障 或 栅栏 47)。
这种行为的原因是每个 CPU 核心都有自己的内存缓存和存储缓冲区。默认情况下,内存访问首先进入缓存,任何更改都异步写出到主内存。由于访问缓存中的数据比访问主内存快得多 48,这个特性对于现代 CPU 的良好性能至关重要。然而,现在有多份数据副本(一份在主内存中,可能还有几份在各种缓存中),这些副本是异步更新的,因此线性一致性丢失了。
为什么要做出这种权衡?使用 CAP 定理来证明多核内存一致性模型是没有意义的:在一台计算机内,我们通常假设可靠的通信,我们不期望一个 CPU 核心在与计算机其余部分断开连接的情况下能够继续正常运行。放弃线性一致性的原因是 性能,而不是容错 39。
许多选择不提供线性一致保证的分布式数据库也是如此:它们这样做主要是为了提高性能,而不是为了容错 42。线性一致性很慢——这在任何时候都是真的,不仅在网络故障期间。
我们能否找到更高效的线性一致存储实现?答案似乎是否定的:Attiya 和 Welch 49 证明,如果你想要线性一致性,读写请求的响应时间至少与网络中延迟的不确定性成正比。在具有高度可变延迟的网络中,例如大多数计算机网络(见 “超时和无界延迟”),线性一致读写的响应时间不可避免地会很高。更快的线性一致性算法不存在,但较弱的一致性模型可能会快得多,因此这种权衡对于延迟敏感的系统很重要。在 [Link to Come] 中,我们将讨论一些在不牺牲正确性的情况下避免线性一致性的方法。
ID 生成器和逻辑时钟
在许多应用程序中,你需要在创建数据库记录时为它们分配某种唯一的 ID,这给了你一个可以引用这些记录的主键。在单节点数据库中,通常使用自增整数,它的优点是只需要 64 位(如果你确定永远不会有超过 40 亿条记录,甚至可以使用 32 位,但这是有风险的)来存储。
这种自增 ID 的另一个优点是,ID 的顺序告诉你记录创建的顺序。例如,图 10-8 显示了一个聊天应用程序,它在发布聊天消息时为其分配自增 ID。然后,你可以按 ID 递增的顺序显示消息,生成的聊天线程将有意义:Aaliyah 发布了一个被分配 ID 1 的问题,而 Bryce 对该问题的回答被分配了一个更大的 ID,即 3。
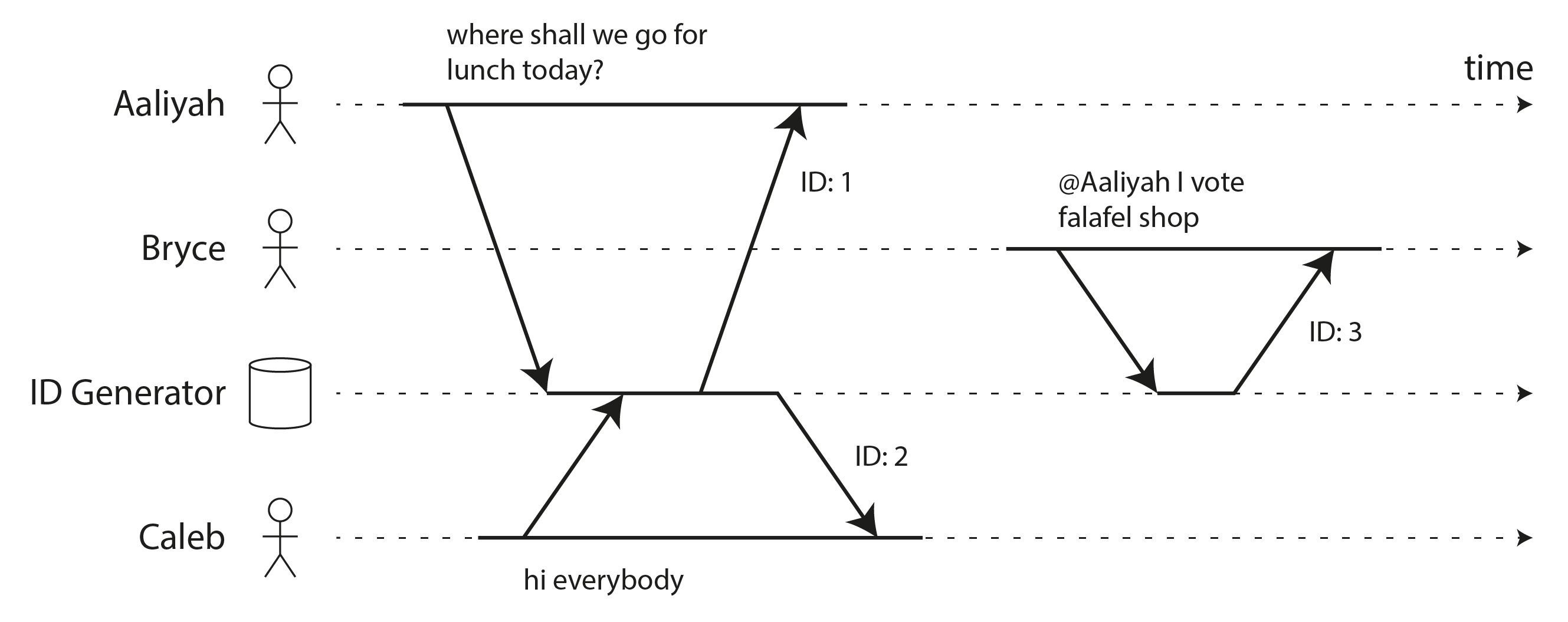
这个单节点 ID 生成器是线性一致系统的另一个例子。每个获取 ID 的请求都是一个原子地递增计数器并返回旧计数器值的操作(获取并增加 操作);线性一致性确保如果 Aaliyah 的消息发布在 Bryce 的发布开始之前完成,那么 Bryce 的 ID 必须大于 Aaliyah 的。图 10-8 中 Aaliyah 和 Caleb 的消息是并发的,因此线性一致性不指定它们的 ID 必须如何排序,只要它们是唯一的。
内存中的单节点 ID 生成器很容易实现:你可以使用 CPU 提供的原子递增指令,它允许多个线程安全地递增同一个计数器。使计数器持久化需要更多的努力,这样节点就可以崩溃并重新启动而不重置计数器值,这将导致重复的 ID。但真正的问题是:
- 单节点 ID 生成器不具容错性,因为该节点是单点故障。
- 如果你想在另一个区域创建记录,速度会很慢,因为你可能必须往返地球的另一端才能获得 ID。
- 如果你有高写入吞吐量,该单个节点可能成为瓶颈。
你可以考虑各种 ID 生成器的替代选项:
- 分片 ID 分配
- 你可以有多个分配 ID 的节点——例如,一个只生成偶数,一个只生成奇数。一般来说,你可以在 ID 中保留一些位来包含分片编号。这些 ID 仍然紧凑,但你失去了排序属性:例如,如果你有 ID 为 16 和 17 的聊天消息,你不知道消息 16 是否实际上是先发送的,因为 ID 是由不同的节点分配的,其中一个节点可能领先于另一个。
- 预分配 ID 块
- 不是从单节点 ID 生成器请求单个 ID,它可以分发 ID 块。例如,节点 A 可能声明从 1 到 1,000 的 ID 块,节点 B 可能声明从 1,001 到 2,000 的块。然后每个节点可以独立地从其块中分发 ID,并在其序列号供应开始不足时从单节点 ID 生成器请求新块。但是,这种方案也不能确保正确的排序:可能会发生这样的情况,一条消息被分配了 1,001 到 2,000 范围内的 ID,而后来的消息被分配了 1 到 1,000 范围内的 ID,如果 ID 是由不同的节点分配的。
- 随机 UUID
- 你可以使用 通用唯一标识符(UUID),也称为 全局唯一标识符(GUID)。它们的一大优点是可以在任何节点上本地生成,无需通信,但它们需要更多空间(128 位)。有几种不同版本的 UUID;最简单的是版本 4,它本质上是一个如此长的随机数,以至于两个节点选择相同的可能性非常小。不幸的是,这些 ID 的顺序也是随机的,因此比较两个 ID 不会告诉你哪个更新。
- 时钟时间戳使其唯一
- 如果你的节点的日历时钟使用 NTP 保持大致正确,你可以通过将该时钟的时间戳放在最高有效位中,并用确保 ID 唯一的额外信息填充剩余位来生成 ID,即使时间戳不是——例如,分片编号和每分片递增序列号,或长随机值。这种方法用于版本 7 UUID 50、Twitter 的 Snowflake 51、ULID 52、Hazelcast 的 Flake ID 生成器、MongoDB ObjectID 和许多类似方案 50。你可以在应用程序代码或数据库中实现这些 ID 生成器 53。
所有这些方案都生成唯一的 ID(至少有足够高的概率,使冲突极其罕见),但它们对 ID 的排序保证比单节点自增方案弱得多。
如 “为事件排序的时间戳” 中所讨论的,时钟时间戳最多只能提供近似排序:如果较早的写入从稍快的时钟获得时间戳,而较晚写入的时间戳来自稍慢的时钟,则时间戳顺序可能与事件实际发生的顺序不一致。由于使用非单调时钟而导致的时钟跳跃,即使单个节点生成的时间戳也可能排序错误。因此,基于时钟时间的 ID 生成器不太可能是线性一致的。
你可以通过依赖高精度时钟同步,使用原子钟或 GPS 接收器来减少这种排序不一致。但如果能够在不依赖特殊硬件的情况下生成唯一且正确排序的 ID 也会很好。这就是 逻辑时钟 的用途。
逻辑时钟
在 “不可靠的时钟” 中,我们讨论了日历时钟和单调时钟。这两种都是 物理时钟:它们测量经过的秒数(或毫秒、微秒等)。
在分布式系统中,通常还使用另一种时钟,称为 逻辑时钟。物理时钟是计算已经过的秒数的硬件设备,而逻辑时钟是计算已发生事件的算法。来自逻辑时钟的时间戳因此不会告诉你现在几点,但你 可以 比较来自逻辑时钟的两个时间戳,以判断哪个更早,哪个更晚。
逻辑时钟的要求通常是:
- 其时间戳紧凑(大小为几个字节)且唯一;
- 你可以比较任意两个时间戳(即它们是 全序 的);并且
- 时间戳的顺序与因果关系 一致:如果操作 A 发生在 B 之前,那么 A 的时间戳小于 B 的时间戳。(我们之前在 ““先发生"关系和并发” 中讨论了因果关系。)
单节点 ID 生成器满足这些要求,但我们刚刚讨论的分布式 ID 生成器不满足因果排序要求。
Lamport 时间戳
幸运的是,有一种生成逻辑时间戳的简单方法,它与因果关系 一致,你可以将其用作分布式 ID 生成器。它被称为 Lamport 时钟,由 Leslie Lamport 在 1978 年提出 54,现在是分布式系统领域被引用最多的论文之一。
图 10-9 显示了 Lamport 时钟如何在 图 10-8 的聊天示例中工作。每个节点都有一个唯一标识符,在 图 10-9 中是名称"Aaliyah”、“Bryce"或"Caleb”,但在实践中可能是随机 UUID 或类似的东西。此外,每个节点都保留它已处理的操作数的计数器。Lamport 时间戳就是一对(计数器,节点 ID)。两个节点有时可能具有相同的计数器值,但通过在时间戳中包含节点 ID,每个时间戳都是唯一的。
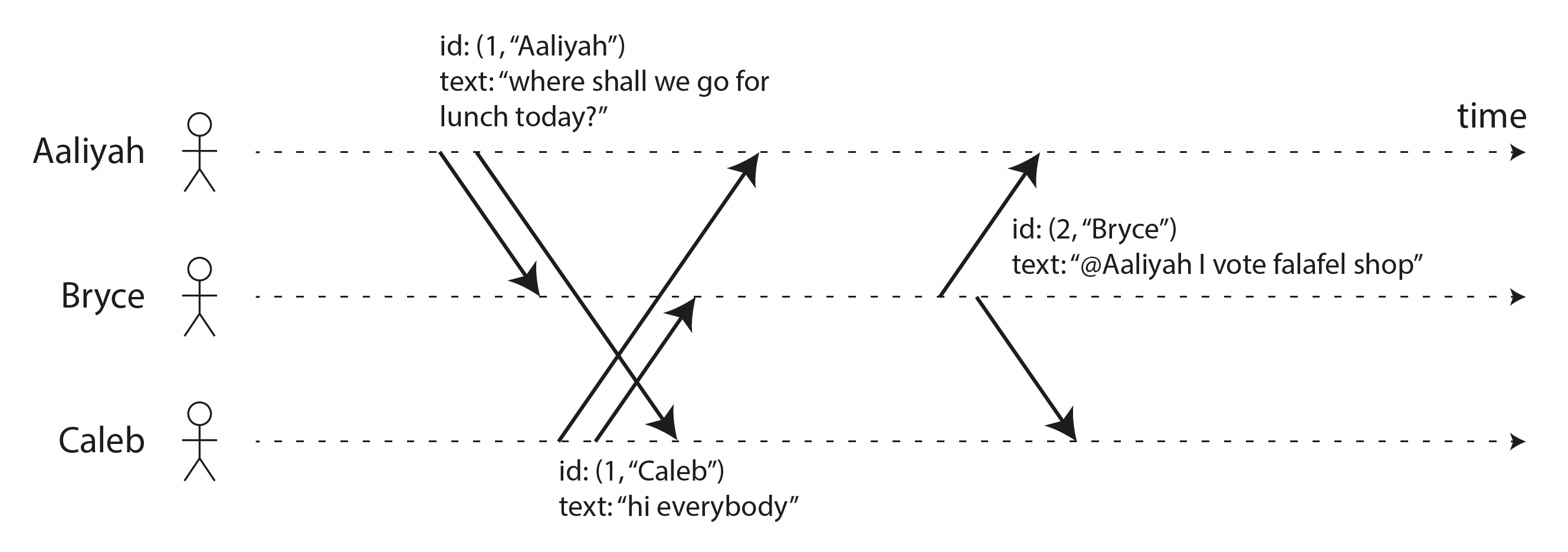
每次节点生成时间戳时,它都会递增其计数器值并使用新值。此外,每次节点看到来自另一个节点的时间戳时,如果该时间戳中的计数器值大于其本地计数器值,它会将其本地计数器增加到与时间戳中的值匹配。
在 图 10-9 中,Aaliyah 在发布自己的消息时还没有看到 Caleb 的消息,反之亦然。假设两个用户都以初始计数器值 0 开始,因此都递增其本地计数器并将新计数器值 1 附加到其消息。当 Bryce 收到这些消息时,他将本地计数器值增加到 1。最后,Bryce 向 Aaliyah 的消息发送回复,为此他递增本地计数器并将新值 2 附加到消息。
要比较两个 Lamport 时间戳,我们首先比较它们的计数器值:例如,(2, “Bryce”) 大于 (1, “Aaliyah”),也大于 (1, “Caleb”)。如果两个时间戳具有相同的计数器,我们改为比较它们的节点 ID,使用通常的字典序字符串比较。因此,此示例中的时间戳顺序是 (1, “Aaliyah”) < (1, “Caleb”) < (2, “Bryce”)。
混合逻辑时钟
Lamport 时间戳擅长捕获事物发生的顺序,但它们有一些限制:
- 由于它们与物理时间没有直接关系,你不能使用它们来查找,比如说,在特定日期发布的所有消息——你需要单独存储物理时间。
- 如果两个节点从不通信,一个节点的计数器递增将永远不会反映在另一个节点的计数器中。因此,可能会发生这样的情况,即在不同节点上大约同一时间生成的事件具有极不相同的计数器值。
混合逻辑时钟 结合了物理日历时钟的优势和 Lamport 时钟的排序保证 55。像物理时钟一样,它计算秒或微秒。像 Lamport 时钟一样,当一个节点看到来自另一个节点的时间戳大于其本地时钟值时,它将自己的本地值向前移动以匹配另一个节点的时间戳。因此,如果一个节点的时钟运行得很快,其他节点在通信时也会类似地向前移动它们的时钟。
每次生成混合逻辑时钟的时间戳时,它也会递增,这确保时钟单调向前移动,即使底层物理时钟由于 NTP 调整而向后跳跃。因此,混合逻辑时钟可能略微领先于底层物理时钟。算法的细节确保这种差异尽可能小。
因此,你可以将混合逻辑时钟的时间戳几乎像传统日历时钟的时间戳一样对待,具有其排序与先发生关系一致的附加属性。它不依赖于任何特殊硬件,只需要大致同步的时钟。例如,CockroachDB 使用混合逻辑时钟。
Lamport/混合逻辑时钟 vs. 向量时钟
在 “多版本并发控制(MVCC)” 中,我们讨论了快照隔离通常是如何实现的:本质上,通过给每个事务一个事务 ID,并允许每个事务看到由 ID 较低的事务进行的写入,但使 ID 较高的事务的写入不可见。Lamport 时钟和混合逻辑时钟是生成这些事务 ID 的好方法,因为它们确保快照与因果关系一致 56。
当并发生成多个时间戳时,这些算法会任意排序它们。这意味着当你查看两个时间戳时,你通常无法判断它们是并发生成的还是一个发生在另一个之前。(在 图 10-9 的示例中,你实际上可以判断 Aaliyah 和 Caleb 的消息必须是并发的,因为它们具有相同的计数器值,但当计数器值不同时,你无法判断它们是否并发。)
如果你想能够确定记录何时并发创建,你需要不同的算法,例如 向量时钟。缺点是向量时钟的时间戳要大得多——可能是系统中每个节点一个整数。有关检测并发的更多详细信息,请参见 “检测并发写入”。
线性一致的 ID 生成器
尽管 Lamport 时钟和混合逻辑时钟提供了有用的排序保证,但该排序仍然弱于我们之前讨论的线性一致单节点 ID 生成器。回想一下,线性一致性要求如果请求 A 在请求 B 开始之前完成,那么 B 必须具有更高的 ID,即使 A 和 B 从未相互通信。另一方面,Lamport 时钟只能确保节点生成的时间戳大于该节点看到的任何其他时间戳,但它不能对它没有看到的时间戳说任何话。
图 10-10 显示了非线性一致 ID 生成器如何导致问题。想象一个社交媒体网站,用户 A 想要与朋友私下分享一张尴尬的照片。A 的账户最初是公开的,但使用他们的笔记本电脑,A 首先将他们的账户设置更改为私密。然后 A 使用他们的手机上传照片。由于 A 按顺序执行了这些更新,他们可能合理地期望照片上传受到新的、受限的账户权限的约束。
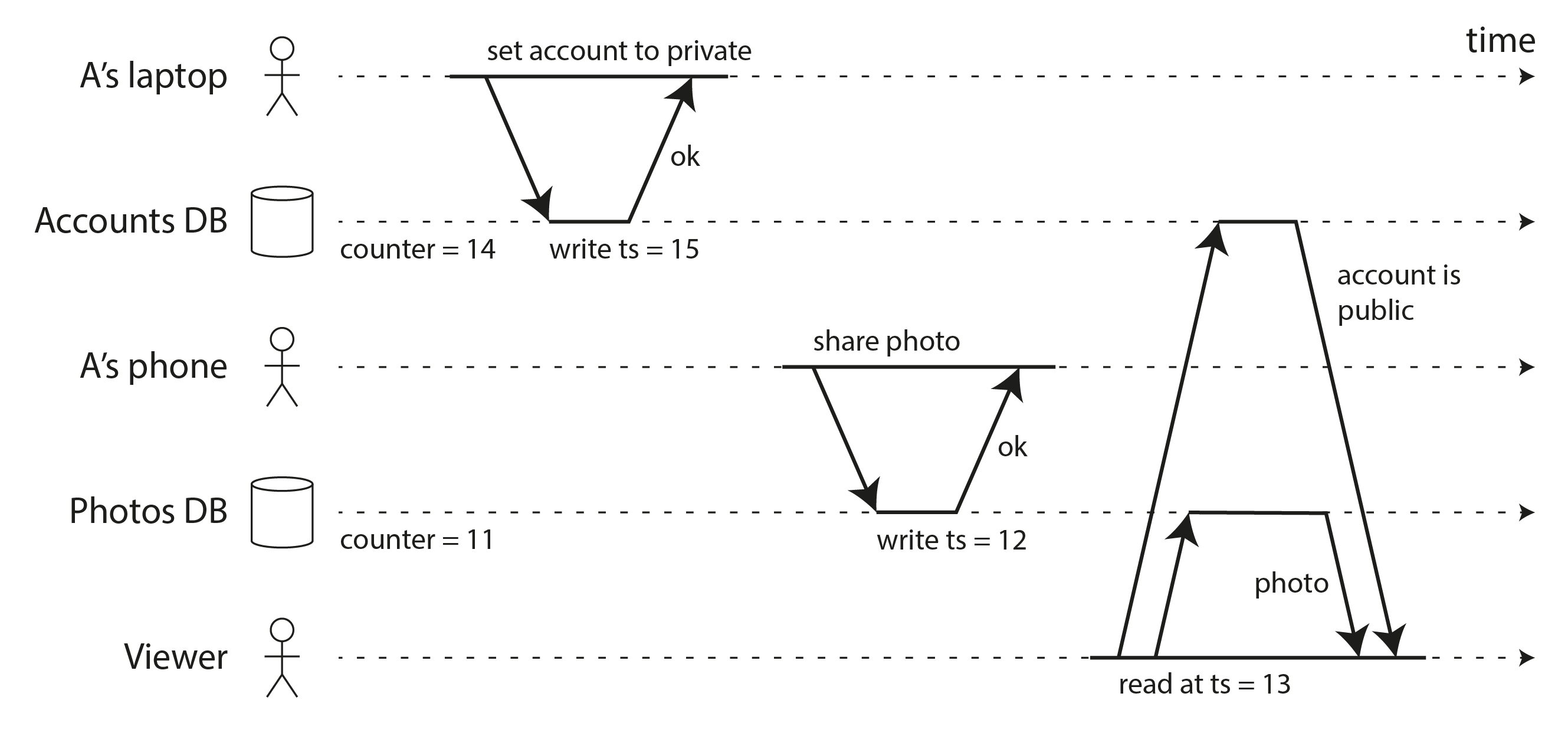
账户权限和照片存储在两个单独的数据库(或同一数据库的单独分片)中,让我们假设它们使用 Lamport 时钟或混合逻辑时钟为每次写入分配时间戳。由于照片数据库没有从账户数据库读取,照片数据库中的本地计数器可能稍微落后,因此照片上传被分配了比账户设置更新更低的时间戳。
接下来,假设一个查看者(不是 A 的朋友)正在查看 A 的个人资料,他们的读取使用快照隔离的 MVCC 实现。可能会发生这样的情况,查看者的读取具有大于照片上传的时间戳,但小于账户设置更新的时间戳。因此,系统将确定在读取时账户仍然是公开的,因此向查看者显示他们不应该看到的尴尬照片。
你可以想象几种可能的方法来解决这个问题。也许照片数据库应该在执行写入之前读取用户的账户状态,但很容易忘记这样的检查。如果 A 的操作是在同一设备上执行的,也许该设备上的应用程序可以跟踪该用户写入的最新时间戳——但如果用户使用笔记本电脑和手机,如示例中所示,那就不那么容易了。
在这种情况下,最简单的解决方案是使用线性一致的 ID 生成器,这将确保照片上传被分配比账户权限更改更大的 ID。
实现线性一致的 ID 生成器
确保 ID 分配线性一致的最简单方法实际上是为此目的使用单个节点。该节点只需要原子地递增计数器并在请求时返回其值,持久化计数器值(以便在节点崩溃并重新启动时不会生成重复的 ID),并使用单主复制进行容错复制。这种方法在实践中使用:例如,TiDB/TiKV 称之为 时间戳预言机,受 Google 的 Percolator 57 启发。
作为优化,你可以避免在每个请求上执行磁盘写入和复制。相反,ID 生成器可以写入描述一批 ID 的记录;一旦该记录被持久化和复制,节点就可以开始按顺序向客户端分发这些 ID。在它用完该批次中的 ID 之前,它可以为下一批持久化和复制记录。这样,如果节点崩溃并重新启动或你故障转移到从节点,某些 ID 将被跳过,但你不会发出任何重复或乱序的 ID。
你不能轻易地对 ID 生成器进行分片,因为如果你有多个分片独立分发 ID,你就无法再保证它们的顺序是线性一致的。你也不能轻易地将 ID 生成器分布在多个区域;因此,在地理分布式数据库中,所有 ID 请求都必须转到单个区域的节点。从好的方面来说,ID 生成器的工作非常简单,因此单个节点可以处理大量请求吞吐量。
如果你不想使用单节点 ID 生成器,可以使用替代方案:你可以做 Google 的 Spanner 所做的,如 “全局快照的同步时钟” 中所讨论的。它依赖于物理时钟,该时钟不仅返回单个时间戳,还返回表示时钟读数不确定性的时间戳范围。然后它等待该不确定性间隔的持续时间过去后再返回。
假设不确定性间隔是正确的(即真实的当前物理时间始终位于该间隔内),此过程还确保如果一个请求在另一个请求开始之前完成,后一个请求将具有更大的时间戳。这种方法确保了这种线性一致的 ID 分配,而无需任何通信:即使不同区域的请求也将被正确排序,无需等待跨区域请求。缺点是你需要硬件和软件支持,以使时钟紧密同步并计算必要的不确定性间隔。
使用逻辑时钟强制约束
在 “约束与唯一性保证” 中,我们看到线性一致的比较并设置操作可用于在分布式系统中实现锁、唯一性约束和类似构造。这提出了一个问题:逻辑时钟或线性一致的 ID 生成器是否也足以实现这些东西?
答案是:不完全。当你有几个节点都试图获取同一个锁或注册同一个用户名时,你可以使用逻辑时钟为这些请求分配时间戳,并选择具有最低时间戳的请求作为获胜者。如果时钟是线性一致的,你知道任何未来的请求都将始终生成更大的时间戳,因此你可以确定没有未来的请求会收到比获胜者更低的时间戳。
不幸的是,问题的一部分仍未解决:节点如何知道自己的时间戳是否最低?要确定,它需要听到可能生成时间戳的 每个 其他节点 54。如果其他节点之一在此期间失败,或者由于网络问题无法访问,该系统将停止运行,因为我们无法确定该节点是否可能具有最低的时间戳。这不是我们需要的那种容错系统。
要以容错方式实现锁、租约和类似构造,我们需要比逻辑时钟或 ID 生成器更强大的东西:我们需要共识。
共识
在本章中,我们已经看到了几个只有单个节点时很容易,但如果你想要容错就会变得困难得多的例子:
- 如果你只有一个主节点,并且在该主节点上进行所有读写,数据库可以是线性一致的。但是,如果该主节点失败,如何进行故障切换,同时避免脑裂?如何确保一个认为自己是主节点的节点实际上没有被投票罢免?
- 单节点上的线性一致 ID 生成器只是一个带有原子获取并增加指令的计数器,但如果它崩溃了怎么办?
- 原子比较并设置(CAS)操作对许多事情都很有用,例如当多个进程竞相获取它时决定谁获得锁或租约,或确保具有给定名称的文件或用户的唯一性。在单个节点上,CAS 可能就像一条 CPU 指令一样简单,但如何使其容错?
事实证明,所有这些都是同一个基本分布式系统问题的实例:共识。共识是分布式计算中最重要和最基本的问题之一;它也是出了名的难以正确实现 58 59,许多系统在过去都出错了。现在我们已经讨论了复制(第六章)、事务(第八章)、系统模型(第九章)和线性一致性(本章),我们终于准备好解决共识问题了。
最著名的共识算法是 Viewstamped Replication 60 61、Paxos 58 62 63 64、Raft 23 65 66 和 Zab 18 22 67。这些算法之间有相当多的相似之处,但它们并不相同 68 69。这些算法在非拜占庭系统模型中工作:也就是说,网络通信可能会被任意延迟或丢弃,节点可能会崩溃、重启和断开连接,但算法假设节点在其他方面正确遵循协议,不会恶意行为。
也有可以容忍某些拜占庭节点的共识算法,即不正确遵循协议的节点(例如,向其他节点发送矛盾消息)。一个常见的假设是少于三分之一的节点是拜占庭故障的 26 70。这种 拜占庭容错(BFT)共识算法用于区块链 71。然而,如 “拜占庭故障” 中所解释的,BFT 算法超出了本书的范围。
共识的不可能性
你可能听说过 FLP 结果 72——以作者 Fischer、Lynch 和 Paterson 的名字命名——它证明如果存在节点可能崩溃的风险,就没有算法总是能够达成共识。在分布式系统中,我们必须假设节点可能会崩溃,因此可靠的共识是不可能的。然而,在这里我们正在讨论实现共识的算法。这是怎么回事?
首先,FLP 并不是说我们永远无法达成共识——它只是说我们不能保证共识算法 总是 终止。此外,FLP 结果是在异步系统模型中假设确定性算法的情况下证明的(见 “系统模型与现实”),这意味着算法不能使用任何时钟或超时。如果它可以使用超时来怀疑另一个节点可能已经崩溃(即使怀疑有时是错误的),那么共识就变得可解 73。即使只是允许算法使用随机数也足以绕过不可能性结果 74。
因此,尽管 FLP 关于共识不可能性的结果具有重要的理论意义,但分布式系统通常可以在实践中实现共识。
共识的多面性
共识可以用几种不同的方式表达:
- 单值共识 非常类似于原子 比较并设置 操作,它可用于实现锁、租约和唯一性约束。
- 构建 仅追加日志 也需要共识;它通常形式化为 全序广播。有了日志,你可以构建 状态机复制、基于主节点的复制、事件溯源和其他有用的东西。
- 多数据库或多分片事务的 原子提交 要求所有参与者就是否提交或中止事务达成一致。
我们很快就会探讨所有这些。事实上,这些问题都是相互等价的:如果你有解决其中一个问题的算法,你可以将其转换为任何其他问题的解决方案。这是一个相当深刻且也许令人惊讶的见解!这就是为什么我们可以将所有这些东西归入"共识"之下,即使它们表面上看起来完全不同。
单值共识
共识的标准表述涉及让多个节点就单个值达成一致。例如:
- 当具有单主复制的数据库首次启动时,或者当现有主节点失败时,多个节点可能会同时尝试成为主节点。同样,多个节点可能竞相获取锁或租约。共识允许它们决定哪一个获胜。
- 如果几个人同时尝试预订飞机上的最后一个座位,或剧院中的同一个座位,或尝试使用相同的用户名注册账户,那么共识算法可以确定哪一个应该成功。
更一般地说,一个或多个节点可能 提议 值,共识算法 决定 其中一个值。在上述示例中,每个节点可以提议自己的 ID,算法决定哪个节点 ID 应该成为新的主节点、租约的持有者或飞机/剧院座位的购买者。在这种形式主义中,共识算法必须满足以下属性 26:
- 一致同意
- 没有两个节点决定不同。
- 完整性
- 一旦节点决定了一个值,它就不能通过决定另一个值来改变主意。
- 有效性
- 如果节点决定值 v,那么 v 是由某个节点提议的。
- 终止
- 每个未崩溃的节点最终都会决定某个值。
如果你想决定多个值,你可以为每个值运行共识算法的单独实例。例如,你可以为剧院中的每个可预订座位进行单独的共识运行,这样你就可以为每个座位获得一个决定(一个买家)。
一致同意和完整性属性定义了共识的核心思想:每个人都决定相同的结果,一旦你决定了,你就不能改变主意。有效性属性排除了琐碎的解决方案:例如,你可以有一个总是决定 null 的算法,无论提议什么;这个算法将满足同意和完整性属性,但不满足有效性属性。
如果你不关心容错,那么满足前三个属性很容易:你可以硬编码一个节点作为"独裁者",让该节点做出所有决定。然而,如果那个节点失败,那么系统就无法再做出任何决定——就像没有故障切换的单主复制一样。所有的困难都来自对容错的需求。
终止属性形式化了容错的想法。它本质上是说共识算法不能简单地坐着什么都不做——换句话说,它必须取得进展。即使某些节点失败,其他节点仍必须达成决定。(终止是活性属性,而其他三个是安全属性——见 “安全性和活性”。)
如果崩溃的节点可能恢复,你可以等待它回来。然而,共识必须确保即使崩溃的节点突然消失并且永远不会回来,它也会做出决定。(不要想象软件崩溃,而是想象有地震,包含你的节点的数据中心被山体滑坡摧毁。你必须假设你的节点被埋在 30 英尺的泥土下,永远不会重新上线。)
当然,如果 所有 节点都崩溃了,并且没有一个在运行,那么任何算法都不可能决定任何事情。算法可以容忍的故障数量是有限的:事实上,可以证明任何共识算法都需要至少大多数节点正常运行才能确保终止 73。该多数可以安全地形成仲裁(见 “读写仲裁”)。
因此,终止属性受到少于一半节点崩溃或不可达的假设的约束。然而,大多数共识算法确保安全属性——同意、完整性和有效性——始终得到满足,即使大多数节点失败或存在严重的网络问题 75。因此,大规模中断可能会阻止系统处理请求,但它不能通过导致做出不一致的决定来破坏共识系统。
比较并设置作为共识
比较并设置(CAS)操作检查某个对象的当前值是否等于某个期望值;如果是,它原子地将对象更新为某个新值;如果不是,它保持对象不变并返回错误。
如果你有容错、线性一致的 CAS 操作,很容易解决共识问题:最初将对象设置为空值;每个想要提议值的节点都使用期望值为空、新值为它想要提议的值(假设它是非空的)调用 CAS。然后决定的值就是对象设置的任何值。
同样,如果你有共识的解决方案,你可以实现 CAS:每当一个或多个节点想要使用相同的期望值执行 CAS 时,你使用共识协议提议 CAS 调用中的新值,然后将对象设置为共识决定的任何值。任何新值未被决定的 CAS 调用都返回错误。具有不同期望值的 CAS 调用使用共识协议的单独运行。
这表明 CAS 和共识彼此等价 28 73。同样,两者在单个节点上都很简单,但要使其容错则具有挑战性。作为分布式环境中 CAS 的示例,我们在 “由对象存储支持的数据库” 中看到了对象存储的条件写入操作,它允许写入仅在自当前客户端上次读取以来具有相同名称的对象未被另一个客户端创建或修改时发生。
然而,线性一致的读写寄存器不足以解决共识。FLP 结果告诉我们,共识不能由异步崩溃停止模型中的确定性算法解决 72,但我们在 “线性一致性与仲裁” 中看到,线性一致的寄存器可以使用此模型中的仲裁读/写来实现 24 25 26。由此可见,线性一致的寄存器无法解决共识。
共享日志作为共识
我们已经看到了几个日志的例子,例如复制日志、事务日志和预写日志。日志存储一系列 日志条目,任何读取它的人都会看到相同顺序的相同条目。有时日志有一个允许追加新条目的单个写入者,但 共享日志 是多个节点可以请求追加条目的日志。单主复制的一个例子:任何客户端都可以要求主节点进行写入,主节点将其追加到复制日志,然后所有从节点按照与主节点相同的顺序应用写入。
更正式地说,共享日志支持两种操作:你可以请求将值添加到日志中,并且可以读取日志中的条目。它必须满足以下属性:
- 最终追加
- 如果节点请求将某个值添加到日志中,并且节点不会崩溃,那么该节点最终必须在日志条目中读取该值。
- 可靠交付
- 没有日志条目丢失:如果一个节点读取某个日志条目,那么最终每个未崩溃的节点也必须读取该日志条目。
- 仅追加
- 一旦节点读取了某个日志条目,它就是不可变的,新的日志条目只能在它之后添加,而不能在之前。节点可能会重新读取日志,在这种情况下,它会以与最初读取它们时相同的顺序看到相同的日志条目(即使节点崩溃并重新启动)。
- 一致性
- 如果两个节点都读取某个日志条目 e,那么在 e 之前,它们必须以相同的顺序读取完全相同的日志条目序列。
- 有效性
- 如果节点读取包含某个值的日志条目,那么某个节点先前请求将该值添加到日志中。
如果你有共享日志的实现,很容易解决共识问题:每个想要提议值的节点都请求将其添加到日志中,第一个日志条目中读回的任何值就是决定的值。由于所有节点以相同的顺序读取日志条目,它们保证就首先交付哪个值达成一致 28。
相反,如果你有共识的解决方案,你可以实现共享日志。细节有点复杂,但基本思想是这样的 73:
- 你为每个未来的日志条目在日志中都有一个槽,并且你为每个这样的槽运行共识算法的单独实例,以决定该条目中应该包含什么值。
- 当节点想要向日志添加值时,它为尚未决定的槽之一提议该值。
- 当共识算法为其中一个槽做出决定,并且所有先前的槽都已经决定时,则决定的值作为新的日志条目追加,并且已经决定的任何连续槽也将其决定的值追加到日志中。
- 如果提议的值未被某个槽选择,想要添加它的节点会通过为稍后的槽提议它来重试。
这表明共识等价于全序广播和共享日志。没有故障切换的单主复制不满足活性要求,因为如果主节点崩溃,它将停止传递消息。像往常一样,挑战在于安全地自动执行故障切换。
获取并增加作为共识
我们在 “线性一致的 ID 生成器” 中看到的线性一致 ID 生成器接近解决共识,但略有不足。我们可以使用获取并增加操作实现这样的 ID 生成器,该操作原子地递增计数器并返回旧的计数器值。
如果你有 CAS 操作,很容易实现获取并增加:首先读取计数器值,然后执行 CAS,其中期望值是你读取的值,新值是该值加一。如果 CAS 失败,你将重试整个过程,直到 CAS 成功。当存在争用时,这比本机获取并增加操作效率低,但在功能上是等效的。由于你可以使用共识实现 CAS,你也可以使用共识实现获取并增加。
相反,如果你有容错的获取并增加操作,你能解决共识问题吗?假设你将计数器初始化为零,每个想要提议值的节点都调用获取并增加操作来递增计数器。由于获取并增加操作是原子的,其中一个节点将读取初始值零,其他节点都将读取至少递增过一次的值。
现在假设读取零的节点是获胜者,它的值被决定。这对于读取零的节点有效,但其他节点有问题:它们知道自己不是获胜者,但它们不知道其他节点中哪一个获胜了。获胜者可以向其他节点发送消息,让它们知道它已经获胜,但如果获胜者在有机会发送此消息之前崩溃了怎么办?在这种情况下,其他节点将被挂起,无法决定任何值,因此共识不会终止。其他节点不能回退到另一个节点,因为读取零的节点可能会回来并正确地决定它提议的值。
一个例外是,如果我们确定不超过两个节点将提议值。在这种情况下,节点可以相互发送它们想要提议的值,然后每个都执行获取并增加操作。读取零的节点决定自己的值,读取一的节点决定另一个节点的值。这解决了两个节点之间的共识问题,这就是为什么我们可以说获取并增加的 共识数 为二 28。相比之下,CAS 和共享日志解决了任意数量节点可能提议值的共识,因此它们的共识数为 ∞(无穷大)。
原子提交作为共识
在 “分布式事务” 中,我们看到了 原子提交 问题,即确保参与分布式事务的数据库或分片都提交或中止事务。我们还看到了 两阶段提交 算法,它依赖于作为单点故障的协调器。
共识和原子提交之间有什么关系?乍一看,它们似乎非常相似——两者都需要节点达成某种形式的一致。然而,有一个重要的区别:对于共识,可以决定提议的任何值,而对于原子提交,如果 任何 参与者投票中止,算法 必须 中止。更准确地说,原子提交需要以下属性 78:
- 一致同意
- 没有两个节点决定不同的结果。
- 完整性
- 一旦节点决定了一个结果,它就不能通过决定另一个结果来改变主意。
- 有效性
- 如果节点决定提交,那么所有节点必须先前投票提交。如果任何节点投票中止,节点必须中止。
- 非平凡性
- 如果所有节点都投票提交,并且没有发生通信超时,那么所有节点必须决定提交。
- 终止
- 每个未崩溃的节点最终都会决定提交或中止。
有效性属性确保事务只有在所有节点都同意时才能提交;非平凡性属性确保算法不能简单地总是中止(但如果任何节点之间的通信超时,它允许中止)。其他三个属性基本上与共识相同。
如果你有共识的解决方案,有多种方法可以解决原子提交 78 79。一种方法是这样的:当你想要提交事务时,每个节点将其提交或中止的投票发送给每个其他节点。从自己和每个其他节点收到提交投票的节点使用共识算法提议"提交";收到中止投票或经历超时的节点使用共识算法提议"中止"。当节点发现共识算法决定了什么时,它会相应地提交或中止。
在这个算法中,只有当所有节点都投票提交时,才会提议"提交"。如果任何节点投票中止,所有共识算法中的提议都将是"中止"。如果所有节点都投票提交但某些通信超时,可能会发生某些节点提议"中止"而其他节点提议"提交";在这种情况下,节点是提交还是中止并不重要,只要它们都做同样的事。
如果你有容错的原子提交协议,你也可以解决共识。每个想要提议值的节点都在节点仲裁上启动事务,并在每个节点上执行单节点 CAS,如果其值尚未被另一个事务设置,则将寄存器设置为提议的值。如果 CAS 成功,节点投票提交,否则投票中止。如果原子提交协议决定提交事务,其值将被决定用于共识;如果原子提交中止,提议节点将使用新事务重试。
这表明原子提交和共识也是彼此等价的。
共识的实践
我们已经看到,单值共识、CAS、共享日志和原子提交都彼此等价:你可以将其中一个的解决方案转换为任何其他的解决方案。这是一个有价值的理论见解,但它没有回答这个问题:在实践中,这些许多共识表述中哪一个最有用?
答案是大多数共识系统提供共享日志,也称为全序广播。Raft、Viewstamped Replication 和 Zab 直接提供共享日志。Paxos 提供单值共识,但在实践中,大多数使用 Paxos 的系统实际上使用称为 Multi-Paxos 的扩展,它也提供共享日志。
使用共享日志
共享日志非常适合数据库复制:如果每个日志条目代表对数据库的写入,并且每个副本使用确定性逻辑以相同的顺序处理相同的写入,那么副本将全部处于一致状态。这个想法被称为 状态机复制 80,它是事件溯源背后的原则,我们在 “事件溯源和 CQRS” 中看到了。共享日志对于流处理也很有用,我们将在 [Link to Come] 中看到。
同样,共享日志可用于实现可串行化事务:如 “实际串行执行” 中所讨论的,如果每个日志条目代表要作为存储过程执行的确定性事务,并且如果每个节点以相同的顺序执行这些事务,那么事务将是可串行化的 81 82。
Note
具有强一致性模型的分片数据库通常为每个分片维护一个单独的日志,这提高了可伸缩性,但限制了它们可以跨分片提供的一致性保证(例如,一致快照、外键引用)。跨分片的可串行化事务是可能的,但需要额外的协调 83。
共享日志也很强大,因为它可以很容易地适应其他形式的共识:
- 我们之前看到了如何使用它来实现单值共识和 CAS:只需决定日志中首先出现的值。
- 如果你想要许多单值共识实例(例如,几个人试图预订的剧院中每个座位一个),请在日志条目中包含座位编号,并决定包含给定座位编号的第一个日志条目。
- 如果你想要原子获取并增加,请将要添加到计数器的数字放入日志条目中,当前计数器值是到目前为止所有日志条目的总和。日志条目上的简单计数器可用于生成栅栏令牌(见 “栅栏化僵尸和延迟请求”);例如,在 ZooKeeper 中,此序列号称为
zxid18。
从单主复制到共识
我们之前看到,如果你有一个单一的"独裁者"节点做出决定,单值共识很容易,同样,如果单个主节点是唯一允许向其追加条目的节点,共享日志也很容易。问题是如果该节点失败如何提供容错。
传统上,具有单主复制的数据库没有解决这个问题:它们将主节点故障切换作为人类管理员必须手动执行的操作。不幸的是,这意味着大量的停机时间,因为人类反应的速度是有限的,并且它不满足共识的终止属性。对于共识,我们要求算法可以自动选择新的主节点。(并非所有共识算法都有主节点,但常用的算法有 84。)
然而,有一个问题。我们之前讨论过脑裂的问题,并说所有节点都需要就谁是主节点达成一致——否则两个不同的节点可能各自认为自己是主节点,从而做出不一致的决定。因此,似乎我们需要共识来选举主节点,而我们需要主节点来解决共识。我们如何摆脱这个难题?
事实上,共识算法不要求在任何时候只有一个主节点。相反,它们做出了较弱的保证:它们定义了一个 纪元编号(在 Paxos 中称为 投票编号,在 Viewstamped Replication 中称为 视图编号,在 Raft 中称为 任期编号)并保证在每个纪元内,主节点是唯一的。
当节点因为在某个超时时间内没有收到主节点的消息而认为当前主节点已死时,它可能会开始投票选举新的主节点。这次选举被赋予一个大于任何先前纪元的新纪元编号。如果两个不同纪元中的两个不同主节点之间存在冲突(也许是因为先前的主节点实际上并没有死),那么具有更高纪元编号的主节点获胜。
在主节点被允许将下一个条目追加到共享日志之前,它必须首先检查是否有其他具有更高纪元编号的主节点可能追加不同的条目。它可以通过从节点仲裁收集投票来做到这一点——通常但不总是大多数节点 85。只有在节点不知道任何其他具有更高纪元的主节点时,节点才会投赞成票。
因此,我们有两轮投票:一次选择主节点,第二次对主节点提议的下一个要追加到日志的条目进行投票。这两次投票的仲裁必须重叠:如果对提议的投票成功,投票支持它的节点中至少有一个也必须参与了最近成功的主节点选举 85。因此,如果对提议的投票通过而没有透露任何更高编号的纪元,当前主节点可以得出结论,没有选出具有更高纪元编号的主节点,因此它可以安全地将提议的条目追加到日志中 26 86。
这两轮投票表面上看起来类似于两阶段提交,但它们是非常不同的协议。在共识算法中,任何节点都可以开始选举,它只需要节点仲裁的响应;在 2PC 中,只有协调器可以请求投票,它需要 每个 参与者的"是"投票才能提交。
共识的微妙之处
这个基本结构对于 Raft、Multi-Paxos、Zab 和 Viewstamped Replication 的所有都是通用的:节点仲裁的投票选举主节点,然后主节点想要追加到日志的每个条目都需要另一个仲裁投票 68 69。每个新的日志条目在确认给请求写入的客户端之前都会同步复制到节点仲裁。这确保如果当前主节点失败,日志条目不会丢失。
然而,魔鬼在细节中,这也是这些算法采用不同方法的地方。例如,当旧主节点失败并选出新主节点时,算法需要确保新主节点遵守旧主节点在失败之前已经追加的任何日志条目。Raft 通过只允许其日志至少与其大多数追随者一样最新的节点成为新主节点来做到这一点 69。相比之下,Paxos 允许任何节点成为新主节点,但要求它在开始追加自己的新条目之前使其日志与其他节点保持最新。
主节点选举中的一致性与可用性
如果你希望共识算法严格保证 “共享日志作为共识” 中列出的属性,那么新主节点在处理任何写入或线性一致读取之前必须了解任何已确认的日志条目,这一点至关重要。如果具有过时数据的节点成为新主节点,它可能会将新值写入已经由旧主节点写入的日志条目,从而违反共享日志的仅追加属性。
在某些情况下,你可能选择削弱共识属性,以便更快地从主节点故障中恢复。例如,Kafka 提供了启用 不干净的主节点选举 的选项,它允许任何副本成为主节点,即使它不是最新的。此外,在具有异步复制的数据库中,当主节点失败时,你无法保证任何从节点是最新的。
如果你放弃新主节点必须是最新的要求,你可能会提高性能和可用性,但你是在薄冰上,因为共识理论不再适用。虽然只要没有故障,事情就会正常工作,但 第九章 中讨论的问题很容易导致大量数据丢失或损坏。
另一个微妙之处是如何处理算法处理旧主节点在失败之前提议的日志条目,但对于追加到日志的投票尚未完成。你可以在本章的参考文献中找到这些细节的讨论 23 69 86。
对于使用共识算法进行复制的数据库,不仅写入需要转换为日志条目并复制到仲裁。如果你想保证线性一致的读取,它们也必须像写入一样通过仲裁投票,以确认认为自己是主节点的节点确实仍然是最新的。例如,etcd 中的线性一致读取就是这样工作的。
在其标准形式中,大多数共识算法假设一组固定的节点——也就是说,节点可能会宕机并重新启动,但允许投票的节点集在创建集群时是固定的。在实践中,通常需要在系统配置中添加新节点或删除旧节点。共识算法已经扩展了 重新配置 功能,使这成为可能。这在向系统添加新区域或从一个位置迁移到另一个位置(通过首先添加新节点,然后删除旧节点)时特别有用。
共识的利弊
尽管它们复杂而微妙,但共识算法是分布式系统的巨大突破。共识本质上是"正确完成的单主复制",在主节点故障时自动故障切换,确保没有已提交的数据丢失,也不可能出现脑裂,即使面对我们在 第九章 中讨论的所有问题。
由于单主复制与自动故障切换本质上是共识的定义之一,任何提供自动故障切换但不使用经过验证的共识算法的系统都可能是不安全的 87。使用经过验证的共识算法并不能保证整个系统的正确性——仍然有很多其他地方可能潜伏着错误——但这是一个好的开始。
然而,共识并不是到处都使用,因为好处是有代价的。共识系统总是需要严格的多数才能运行——容忍一个故障需要三个节点,或者容忍两个故障需要五个节点。每个操作都需要与仲裁通信,因此你不能通过添加更多节点来增加吞吐量(事实上,你添加的每个节点都会使算法变慢)。如果网络分区将某些节点与其余节点隔离,只有网络的多数部分可以取得进展,其余部分被阻塞。
共识系统通常依赖超时来检测失败的节点。在具有高度可变网络延迟的环境中,特别是跨多个地理区域分布的系统,调整这些超时可能很困难:如果它们太大,从故障中恢复需要很长时间;如果它们太小,可能会有很多不必要的主节点选举,导致糟糕的性能,因为系统最终花费更多时间选择主节点而不是做有用的工作。
有时,共识算法对网络问题特别敏感。例如,Raft 已被证明具有不愉快的边缘情况 88 89:如果除了一个始终不可靠的特定网络链接之外,整个网络都正常工作,Raft 可能会进入主节点身份在两个节点之间不断跳跃的情况,或者当前主节点不断被迫辞职,因此系统实际上从未取得进展。设计对不可靠网络更稳健的算法仍然是一个开放的研究问题。
对于想要高可用但不想接受共识成本的系统,唯一真正的选择是使用较弱的一致性模型,例如 第六章 中讨论的无主或多主复制提供的模型。这些方法通常不提供线性一致性,但对于不需要它的应用程序来说这很好。
总结
在本章中,我们研究了容错系统中强一致性的主题:它是什么,以及如何实现它。我们深入研究了线性一致性,这是强一致性的一种流行形式化:它意味着复制的数据看起来好像只有一个副本,所有操作都以原子方式作用于它。我们看到,当你需要在读取时某些数据是最新的,或者需要解决竞争条件(例如,如果多个节点并发地尝试做同样的事情,比如创建具有相同名称的文件)时,线性一致性是有用的。
虽然线性一致性很有吸引力,因为它易于理解——它使数据库的行为像单线程程序中的变量一样——但它的缺点是速度慢,特别是在网络延迟较大的环境中。许多复制算法不能保证线性一致性,即使表面上看起来它们可能提供强一致性。
接下来,我们在 ID 生成器的背景下应用了线性一致性的概念。单节点自增计数器是线性一致的,但不是容错的。许多分布式 ID 生成方案不能保证 ID 的顺序与事件实际发生的顺序一致。像 Lamport 时钟和混合逻辑时钟这样的逻辑时钟提供了与因果关系一致的顺序,但没有线性一致性。
这引导我们进入了共识的概念。我们看到,达成共识意味着以一种所有节点都同意决定的方式决定某事,并且他们不能改变主意。广泛的问题实际上可以归约为共识,并且彼此等价(即,如果你有一个问题的解决方案,你可以将其转换为所有其他问题的解决方案)。这些等价的问题包括:
- 线性一致的比较并设置操作
- 寄存器需要根据其当前值是否等于操作中给定的参数,原子地 决定 是否设置其值。
- 锁和租约
- 当多个客户端并发地尝试获取锁或租约时,锁 决定 哪一个成功获取它。
- 唯一性约束
- 当多个事务并发地尝试创建具有相同键的冲突记录时,约束必须 决定 允许哪一个,哪一个应该因约束违反而失败。
- 共享日志
- 当多个节点并发地想要向日志追加条目时,日志 决定 它们被追加的顺序。全序广播也是等价的。
- 原子事务提交
- 参与分布式事务的数据库节点必须都以相同的方式 决定 是提交还是中止事务。
- 线性一致的 fetch-and-add 操作
- 这个操作可以用来实现 ID 生成器。多个节点可以并发地调用该操作,它 决定 它们递增计数器的顺序。这种情况实际上只解决了两个节点之间的共识,而其他的适用于任意数量的节点。
如果你只有一个节点,或者如果你愿意将决策能力分配给单个节点,所有这些都是简单的。这就是单领导者数据库中发生的事情:所有的决策权都授予了领导者,这就是为什么这样的数据库能够提供线性一致的操作、唯一性约束、复制日志等等。
然而,如果那个单一的领导者失败,或者如果网络中断使领导者无法访问,这样的系统就无法取得任何进展,直到人工执行手动故障转移。广泛使用的共识算法如 Raft 和 Paxos 本质上是带有内置自动领导者选举和故障转移的单领导者复制(如果当前领导者失败)。
共识算法经过精心设计,以确保在故障转移期间不会丢失任何已提交的写入,并且系统不会进入脑裂状态(多个节点接受写入)。这要求每个写入和每个线性一致的读取都由节点的仲裁(通常是多数)确认。这可能是昂贵的,特别是跨地理区域,但如果你想要共识提供的强一致性和容错性,这是不可避免的。
像 ZooKeeper 和 etcd 这样的协调服务也是建立在共识算法之上的。它们提供锁、租约、故障检测和变更通知功能,这些功能对于管理分布式应用程序的状态很有用。如果你发现自己想要做那些可以归约为共识的事情之一,并且你希望它是容错的,建议使用协调服务。它不会保证你做对,但它可能会有所帮助。
共识算法是复杂而微妙的,但它们得到了自 1980 年代以来发展起来的丰富理论体系的支持。这个理论使得构建能够容忍我们在第 9 章中讨论的所有故障的系统成为可能,同时仍然确保你的数据不会损坏。这是一个了不起的成就,本章末尾的参考文献展示了这项工作的一些亮点。
然而,共识并不总是正确的工具:在某些系统中,不需要它提供的强一致性属性,使用较弱的一致性以获得更高的可用性和更好的性能会更好。在这些情况下,通常使用无领导者或多领导者复制,这是我们之前在第 6 章中讨论过的。我们在本章中讨论的逻辑时钟在那种情况下是有帮助的。
参考文献
Maurice P. Herlihy and Jeannette M. Wing. Linearizability: A Correctness Condition for Concurrent Objects. ACM Transactions on Programming Languages and Systems (TOPLAS), volume 12, issue 3, pages 463–492, July 1990. doi:10.1145/78969.78972 ↩︎ ↩︎
Leslie Lamport. On interprocess communication. Distributed Computing, volume 1, issue 2, pages 77–101, June 1986. doi:10.1007/BF01786228 ↩︎
David K. Gifford. Information Storage in a Decentralized Computer System. Xerox Palo Alto Research Centers, CSL-81-8, June 1981. Archived at perma.cc/2XXP-3JPB ↩︎
Martin Kleppmann. Please Stop Calling Databases CP or AP. martin.kleppmann.com, May 2015. Archived at perma.cc/MJ5G-75GL ↩︎ ↩︎ ↩︎
Kyle Kingsbury. Call Me Maybe: MongoDB Stale Reads. aphyr.com, April 2015. Archived at perma.cc/DXB4-J4JC ↩︎
Kyle Kingsbury. Computational Techniques in Knossos. aphyr.com, May 2014. Archived at perma.cc/2X5M-EHTU ↩︎
Kyle Kingsbury and Peter Alvaro. Elle: Inferring Isolation Anomalies from Experimental Observations. Proceedings of the VLDB Endowment, volume 14, issue 3, pages 268–280, November 2020. doi:10.14778/3430915.3430918 ↩︎
Paolo Viotti and Marko Vukolić. Consistency in Non-Transactional Distributed Storage Systems. ACM Computing Surveys (CSUR), volume 49, issue 1, article no. 19, June 2016. doi:10.1145/2926965 ↩︎ ↩︎
Peter Bailis. Linearizability Versus Serializability. bailis.org, September 2014. Archived at perma.cc/386B-KAC3 ↩︎
Daniel Abadi. Correctness Anomalies Under Serializable Isolation. dbmsmusings.blogspot.com, June 2019. Archived at perma.cc/JGS7-BZFY ↩︎
Peter Bailis, Aaron Davidson, Alan Fekete, Ali Ghodsi, Joseph M. Hellerstein, and Ion Stoica. Highly Available Transactions: Virtues and Limitations. Proceedings of the VLDB Endowment, volume 7, issue 3, pages 181–192, November 2013. doi:10.14778/2732232.2732237, extended version published as arXiv:1302.0309 ↩︎
Philip A. Bernstein, Vassos Hadzilacos, and Nathan Goodman. Concurrency Control and Recovery in Database Systems. Addison-Wesley, 1987. ISBN: 978-0-201-10715-9, available online at microsoft.com. ↩︎
Andrei Matei. CockroachDB’s consistency model. cockroachlabs.com, February 2021. Archived at perma.cc/MR38-883B ↩︎
Murat Demirbas. Strict-serializability, but at what cost, for what purpose? muratbuffalo.blogspot.com, August 2022. Archived at perma.cc/T8AY-N3U9 ↩︎
Ben Darnell. How to talk about consistency and isolation in distributed DBs. cockroachlabs.com, February 2022. Archived at perma.cc/53SV-JBGK ↩︎
Daniel Abadi. An explanation of the difference between Isolation levels vs. Consistency levels. dbmsmusings.blogspot.com, August 2019. Archived at perma.cc/QSF2-CD4P ↩︎
Mike Burrows. The Chubby Lock Service for Loosely-Coupled Distributed Systems. At 7th USENIX Symposium on Operating System Design and Implementation (OSDI), November 2006. ↩︎
Flavio P. Junqueira and Benjamin Reed. ZooKeeper: Distributed Process Coordination. O’Reilly Media, 2013. ISBN: 978-1-449-36130-3 ↩︎ ↩︎ ↩︎ ↩︎
Murali Vallath. Oracle 10g RAC Grid, Services & Clustering. Elsevier Digital Press, 2006. ISBN: 978-1-555-58321-7 ↩︎ ↩︎
Peter Bailis, Alan Fekete, Michael J. Franklin, Ali Ghodsi, Joseph M. Hellerstein, and Ion Stoica. Coordination Avoidance in Database Systems. Proceedings of the VLDB Endowment, volume 8, issue 3, pages 185–196, November 2014. doi:10.14778/2735508.2735509 ↩︎
Kyle Kingsbury. Call Me Maybe: etcd and Consul. aphyr.com, June 2014. Archived at perma.cc/XL7U-378K ↩︎
Flavio P. Junqueira, Benjamin C. Reed, and Marco Serafini. Zab: High-Performance Broadcast for Primary-Backup Systems. At 41st IEEE International Conference on Dependable Systems and Networks (DSN), June 2011. doi:10.1109/DSN.2011.5958223 ↩︎ ↩︎
Diego Ongaro and John K. Ousterhout. In Search of an Understandable Consensus Algorithm. At USENIX Annual Technical Conference (ATC), June 2014. ↩︎ ↩︎ ↩︎
Hagit Attiya, Amotz Bar-Noy, and Danny Dolev. Sharing Memory Robustly in Message-Passing Systems. Journal of the ACM, volume 42, issue 1, pages 124–142, January 1995. doi:10.1145/200836.200869 ↩︎ ↩︎
Nancy Lynch and Alex Shvartsman. Robust Emulation of Shared Memory Using Dynamic Quorum-Acknowledged Broadcasts. At 27th Annual International Symposium on Fault-Tolerant Computing (FTCS), June 1997. doi:10.1109/FTCS.1997.614100 ↩︎ ↩︎
Christian Cachin, Rachid Guerraoui, and Luís Rodrigues. Introduction to Reliable and Secure Distributed Programming, 2nd edition. Springer, 2011. ISBN: 978-3-642-15259-7, doi:10.1007/978-3-642-15260-3 ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
Niklas Ekström, Mikhail Panchenko, and Jonathan Ellis. Possible Issue with Read Repair? Email thread on cassandra-dev mailing list, October 2012. ↩︎
Maurice P. Herlihy. Wait-Free Synchronization. ACM Transactions on Programming Languages and Systems (TOPLAS), volume 13, issue 1, pages 124–149, January 1991. doi:10.1145/114005.102808 ↩︎ ↩︎ ↩︎ ↩︎
Armando Fox and Eric A. Brewer. Harvest, Yield, and Scalable Tolerant Systems. At 7th Workshop on Hot Topics in Operating Systems (HotOS), March 1999. doi:10.1109/HOTOS.1999.798396 ↩︎
Seth Gilbert and Nancy Lynch. Brewer’s Conjecture and the Feasibility of Consistent, Available, Partition-Tolerant Web Services. ACM SIGACT News, volume 33, issue 2, pages 51–59, June 2002. doi:10.1145/564585.564601 ↩︎ ↩︎ ↩︎
Seth Gilbert and Nancy Lynch. Perspectives on the CAP Theorem. IEEE Computer Magazine, volume 45, issue 2, pages 30–36, February 2012. doi:10.1109/MC.2011.389 ↩︎
Eric A. Brewer. CAP Twelve Years Later: How the ‘Rules’ Have Changed. IEEE Computer Magazine, volume 45, issue 2, pages 23–29, February 2012. doi:10.1109/MC.2012.37 ↩︎ ↩︎
Susan B. Davidson, Hector Garcia-Molina, and Dale Skeen. Consistency in Partitioned Networks. ACM Computing Surveys, volume 17, issue 3, pages 341–370, September 1985. doi:10.1145/5505.5508 ↩︎
Paul R. Johnson and Robert H. Thomas. RFC 677: The Maintenance of Duplicate Databases. Network Working Group, January 1975. ↩︎
Michael J. Fischer and Alan Michael. Sacrificing Serializability to Attain High Availability of Data in an Unreliable Network. At 1st ACM Symposium on Principles of Database Systems (PODS), March 1982. doi:10.1145/588111.588124 ↩︎
Eric A. Brewer. NoSQL: Past, Present, Future. At QCon San Francisco, November 2012. ↩︎
Adrian Cockcroft. Migrating to Microservices. At QCon London, March 2014. ↩︎
Martin Kleppmann. A Critique of the CAP Theorem. arXiv:1509.05393, September 2015. ↩︎ ↩︎
Daniel Abadi. Problems with CAP, and Yahoo’s little known NoSQL system. dbmsmusings.blogspot.com, April 2010. Archived at perma.cc/4NTZ-CLM9 ↩︎ ↩︎ ↩︎
Daniel Abadi. Hazelcast and the Mythical PA/EC System. dbmsmusings.blogspot.com, October 2017. Archived at perma.cc/J5XM-U5C2 ↩︎ ↩︎
Eric Brewer. Spanner, TrueTime & The CAP Theorem. research.google.com, February 2017. Archived at perma.cc/59UW-RH7N ↩︎
Daniel J. Abadi. Consistency Tradeoffs in Modern Distributed Database System Design. IEEE Computer Magazine, volume 45, issue 2, pages 37–42, February 2012. doi:10.1109/MC.2012.33 ↩︎ ↩︎
Nancy A. Lynch. A Hundred Impossibility Proofs for Distributed Computing. At 8th ACM Symposium on Principles of Distributed Computing (PODC), August 1989. doi:10.1145/72981.72982 ↩︎
Prince Mahajan, Lorenzo Alvisi, and Mike Dahlin. Consistency, Availability, and Convergence. University of Texas at Austin, Department of Computer Science, Tech Report UTCS TR-11-22, May 2011. Archived at perma.cc/SAV8-9JAJ ↩︎
Hagit Attiya, Faith Ellen, and Adam Morrison. Limitations of Highly-Available Eventually-Consistent Data Stores. At ACM Symposium on Principles of Distributed Computing (PODC), July 2015. doi:10.1145/2767386.2767419 ↩︎
Peter Sewell, Susmit Sarkar, Scott Owens, Francesco Zappa Nardelli, and Magnus O. Myreen. x86-TSO: A Rigorous and Usable Programmer’s Model for x86 Multiprocessors. Communications of the ACM, volume 53, issue 7, pages 89–97, July 2010. doi:10.1145/1785414.1785443 ↩︎
Martin Thompson. Memory Barriers/Fences. mechanical-sympathy.blogspot.co.uk, July 2011. Archived at perma.cc/7NXM-GC5U ↩︎
Ulrich Drepper. What Every Programmer Should Know About Memory. akkadia.org, November 2007. Archived at perma.cc/NU6Q-DRXZ ↩︎
Hagit Attiya and Jennifer L. Welch. Sequential Consistency Versus Linearizability. ACM Transactions on Computer Systems (TOCS), volume 12, issue 2, pages 91–122, May 1994. doi:10.1145/176575.176576 ↩︎
Kyzer R. Davis, Brad G. Peabody, and Paul J. Leach. Universally Unique IDentifiers (UUIDs). RFC 9562, IETF, May 2024. ↩︎ ↩︎
Ryan King. Announcing Snowflake. blog.x.com, June 2010. Archived at archive.org ↩︎
Alizain Feerasta. Universally Unique Lexicographically Sortable Identifier. github.com, 2016. Archived at perma.cc/NV2Y-ZP8U ↩︎
Rob Conery. A Better ID Generator for PostgreSQL. bigmachine.io, May 2014. Archived at perma.cc/K7QV-3KFC ↩︎
Leslie Lamport. Time, Clocks, and the Ordering of Events in a Distributed System. Communications of the ACM, volume 21, issue 7, pages 558–565, July 1978. doi:10.1145/359545.359563 ↩︎ ↩︎
Sandeep S. Kulkarni, Murat Demirbas, Deepak Madeppa, Bharadwaj Avva, and Marcelo Leone. Logical Physical Clocks. 18th International Conference on Principles of Distributed Systems (OPODIS), December 2014. doi:10.1007/978-3-319-14472-6_2 ↩︎
Manuel Bravo, Nuno Diegues, Jingna Zeng, Paolo Romano, and Luís Rodrigues. On the use of Clocks to Enforce Consistency in the Cloud. IEEE Data Engineering Bulletin, volume 38, issue 1, pages 18–31, March 2015. Archived at perma.cc/68ZU-45SH ↩︎
Daniel Peng and Frank Dabek. Large-Scale Incremental Processing Using Distributed Transactions and Notifications. At 9th USENIX Conference on Operating Systems Design and Implementation (OSDI), October 2010. ↩︎
Tushar Deepak Chandra, Robert Griesemer, and Joshua Redstone. Paxos Made Live – An Engineering Perspective. At 26th ACM Symposium on Principles of Distributed Computing (PODC), June 2007. doi:10.1145/1281100.1281103 ↩︎ ↩︎
Will Portnoy. Lessons Learned from Implementing Paxos. blog.willportnoy.com, June 2012. Archived at perma.cc/QHD9-FDD2 ↩︎
Brian M. Oki and Barbara H. Liskov. Viewstamped Replication: A New Primary Copy Method to Support Highly-Available Distributed Systems. At 7th ACM Symposium on Principles of Distributed Computing (PODC), August 1988. doi:10.1145/62546.62549 ↩︎
Barbara H. Liskov and James Cowling. Viewstamped Replication Revisited. Massachusetts Institute of Technology, Tech Report MIT-CSAIL-TR-2012-021, July 2012. Archived at perma.cc/56SJ-WENQ ↩︎
Leslie Lamport. The Part-Time Parliament. ACM Transactions on Computer Systems, volume 16, issue 2, pages 133–169, May 1998. doi:10.1145/279227.279229 ↩︎
Leslie Lamport. Paxos Made Simple. ACM SIGACT News, volume 32, issue 4, pages 51–58, December 2001. Archived at perma.cc/82HP-MNKE ↩︎
Robbert van Renesse and Deniz Altinbuken. Paxos Made Moderately Complex. ACM Computing Surveys (CSUR), volume 47, issue 3, article no. 42, February 2015. doi:10.1145/2673577 ↩︎
Diego Ongaro. Consensus: Bridging Theory and Practice. PhD Thesis, Stanford University, August 2014. Archived at perma.cc/5VTZ-2ADH ↩︎
Heidi Howard, Malte Schwarzkopf, Anil Madhavapeddy, and Jon Crowcroft. Raft Refloated: Do We Have Consensus? ACM SIGOPS Operating Systems Review, volume 49, issue 1, pages 12–21, January 2015. doi:10.1145/2723872.2723876 ↩︎
André Medeiros. ZooKeeper’s Atomic Broadcast Protocol: Theory and Practice. Aalto University School of Science, March 2012. Archived at perma.cc/FVL4-JMVA ↩︎
Robbert van Renesse, Nicolas Schiper, and Fred B. Schneider. Vive La Différence: Paxos vs. Viewstamped Replication vs. Zab. IEEE Transactions on Dependable and Secure Computing, volume 12, issue 4, pages 472–484, September 2014. doi:10.1109/TDSC.2014.2355848 ↩︎ ↩︎
Heidi Howard and Richard Mortier. Paxos vs Raft: Have we reached consensus on distributed consensus?. At 7th Workshop on Principles and Practice of Consistency for Distributed Data (PaPoC), April 2020. doi:10.1145/3380787.3393681 ↩︎ ↩︎ ↩︎ ↩︎
Miguel Castro and Barbara H. Liskov. Practical Byzantine Fault Tolerance and Proactive Recovery. ACM Transactions on Computer Systems, volume 20, issue 4, pages 396–461, November 2002. doi:10.1145/571637.571640 ↩︎
Shehar Bano, Alberto Sonnino, Mustafa Al-Bassam, Sarah Azouvi, Patrick McCorry, Sarah Meiklejohn, and George Danezis. SoK: Consensus in the Age of Blockchains. At 1st ACM Conference on Advances in Financial Technologies (AFT), October 2019. doi:10.1145/3318041.3355458 ↩︎
Michael J. Fischer, Nancy Lynch, and Michael S. Paterson. Impossibility of Distributed Consensus with One Faulty Process. Journal of the ACM, volume 32, issue 2, pages 374–382, April 1985. doi:10.1145/3149.214121 ↩︎ ↩︎
Tushar Deepak Chandra and Sam Toueg. Unreliable Failure Detectors for Reliable Distributed Systems. Journal of the ACM, volume 43, issue 2, pages 225–267, March 1996. doi:10.1145/226643.226647 ↩︎ ↩︎ ↩︎ ↩︎
Michael Ben-Or. Another Advantage of Free Choice: Completely Asynchronous Agreement Protocols. At 2nd ACM Symposium on Principles of Distributed Computing (PODC), August 1983. doi:10.1145/800221.806707 ↩︎
Cynthia Dwork, Nancy Lynch, and Larry Stockmeyer. Consensus in the Presence of Partial Synchrony. Journal of the ACM, volume 35, issue 2, pages 288–323, April 1988. doi:10.1145/42282.42283 ↩︎
Xavier Défago, André Schiper, and Péter Urbán. Total Order Broadcast and Multicast Algorithms: Taxonomy and Survey. ACM Computing Surveys, volume 36, issue 4, pages 372–421, December 2004. doi:10.1145/1041680.1041682 ↩︎
Hagit Attiya and Jennifer Welch. Distributed Computing: Fundamentals, Simulations and Advanced Topics, 2nd edition. John Wiley & Sons, 2004. ISBN: 978-0-471-45324-6, doi:10.1002/0471478210 ↩︎
Rachid Guerraoui. Revisiting the Relationship Between Non-Blocking Atomic Commitment and Consensus. At 9th International Workshop on Distributed Algorithms (WDAG), September 1995. doi:10.1007/BFb0022140 ↩︎ ↩︎
Jim N. Gray and Leslie Lamport. Consensus on Transaction Commit. ACM Transactions on Database Systems (TODS), volume 31, issue 1, pages 133–160, March 2006. doi:10.1145/1132863.1132867 ↩︎
Fred B. Schneider. Implementing Fault-Tolerant Services Using the State Machine Approach: A Tutorial. ACM Computing Surveys, volume 22, issue 4, pages 299–319, December 1990. doi:10.1145/98163.98167 ↩︎
Alexander Thomson, Thaddeus Diamond, Shu-Chun Weng, Kun Ren, Philip Shao, and Daniel J. Abadi. Calvin: Fast Distributed Transactions for Partitioned Database Systems. At ACM International Conference on Management of Data (SIGMOD), May 2012. doi:10.1145/2213836.2213838 ↩︎
Mahesh Balakrishnan, Dahlia Malkhi, Ted Wobber, Ming Wu, Vijayan Prabhakaran, Michael Wei, John D. Davis, Sriram Rao, Tao Zou, and Aviad Zuck. Tango: Distributed Data Structures over a Shared Log. At 24th ACM Symposium on Operating Systems Principles (SOSP), November 2013. doi:10.1145/2517349.2522732 ↩︎
Mahesh Balakrishnan, Dahlia Malkhi, Vijayan Prabhakaran, Ted Wobber, Michael Wei, and John D. Davis. CORFU: A Shared Log Design for Flash Clusters. At 9th USENIX Symposium on Networked Systems Design and Implementation (NSDI), April 2012. ↩︎
Vasilis Gavrielatos, Antonios Katsarakis, and Vijay Nagarajan. Odyssey: the impact of modern hardware on strongly-consistent replication protocols. At 16th European Conference on Computer Systems (EuroSys), April 2021. doi:10.1145/3447786.3456240 ↩︎
Heidi Howard, Dahlia Malkhi, and Alexander Spiegelman. Flexible Paxos: Quorum Intersection Revisited. At 20th International Conference on Principles of Distributed Systems (OPODIS), December 2016. doi:10.4230/LIPIcs.OPODIS.2016.25 ↩︎ ↩︎
Martin Kleppmann. Distributed Systems lecture notes. University of Cambridge, October 2024. Archived at perma.cc/SS3Q-FNS5 ↩︎ ↩︎
Kyle Kingsbury. Call Me Maybe: Elasticsearch 1.5.0. aphyr.com, April 2015. Archived at perma.cc/37MZ-JT7H ↩︎
Heidi Howard and Jon Crowcroft. Coracle: Evaluating Consensus at the Internet Edge. At Annual Conference of the ACM Special Interest Group on Data Communication (SIGCOMM), August 2015. doi:10.1145/2829988.2790010 ↩︎
Tom Lianza and Chris Snook. A Byzantine failure in the real world. blog.cloudflare.com, November 2020. Archived at perma.cc/83EZ-ALCY ↩︎